fantasmes spiralés
Les spirales de Fibonacci
sources :
On retrouve ce texte sous forme d’un ibook (ipad et mac) plus attentivement mis à jour ici.
Exemple typique de truc suffisamment épatant pour devenir un important générateur de fantasmes. Son cadre : la phyllotaxie, l’arrangement (taxis) des feuilles (phyllo).
De très nombreuses plantes présentent des arrangements en spirales de leurs feuilles, de leurs écailles, de leurs pétales, de leurs fleurons ou autre (?).
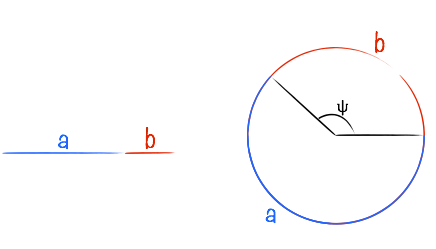
On s’imagine bien que chaque élément nait l’un après l’autre puis s’écarte radialement au fur et à mesure de la croissance de la plante. La présence de spirales laisse supposer un lien fixe entre l’écartement radial et l’angle entre deux éléments consécutifs, entre ri et θi en coordonnées polaires (i=1 correspond à l’élément le plus éloigné, i=2 est un peu plus proche du centre, etc.). Et effectivement, l’observation indique que l’angle entre deux éléments successifs θi+1 - θi est constant. Plus intéressant encore, sa valeur vaut très souvent 137,5° environ. Ça ne vous dit rien ? C’est l’angle d’or ψ ! Nombre et angle d’or, ces immenses pourvoyeurs d’élucubrations.
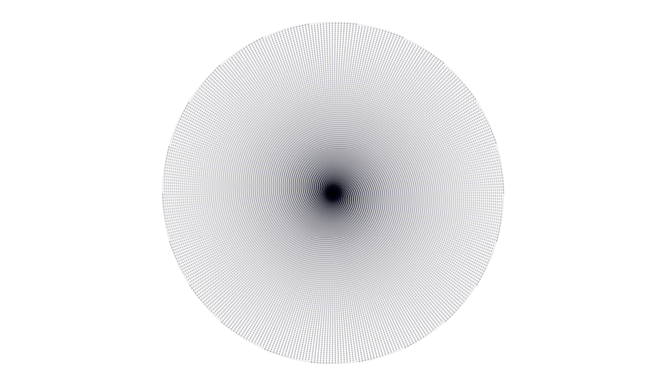
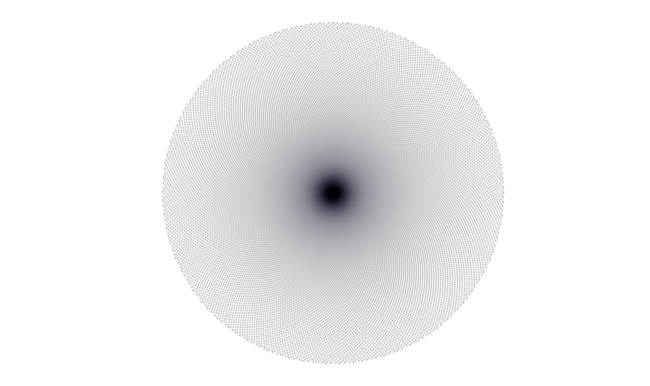
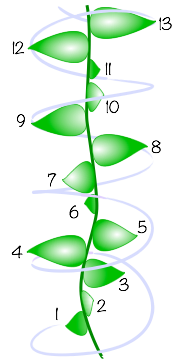
Et si on s’amuse à compter les spirales, la machine à fantasme s’affole. En général, on isole facilement un jeu de spirales dans un sens et un deuxième dans l’autre sens. Leur décompte donne quasi systématiquement les mêmes paires : 8 et 13, 13 et 21, 21 et 34, 34 et 55, 55 et 89... Toujours deux nombres consécutifs de la suite de Fibonacci (un+1 = un + un-1 avec u0=0 et u1=1 donnant un = 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, etc. Cette suite fut d’abord étudié par Fibonacci pour déterminer les populations de lapin après n générations). Plutôt curieux non ?

Quelques précisions pour ceux qui ne seraient pas initiés à ces nombres dorés et à ces suites de lapins. L’angle d’or transfert au cercle la propriété du nombre d’or φ pour les longueurs : le nombre d’or est tel que a/b=(a+b)/a=φ et de même le rapport de la longueur du grand arc a sur la longueur du cercle (a+b) est égal au rapport des longueurs du petit arc de cercle b sur le grand arc a.
Le nombre d’or est le nombre vers lequel tend le rapport de deux nombres consécutifs de la suite de Fibonacci :
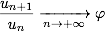
On obtient sa valeur en supposant que pour un assez grand n, un+1/un = un/un-1 = φ. En divisant l’égalité définissant la suite par un, on se retrouve avec un trinôme du second degré en φ dont la solution positive est :
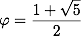
Et cela donne bien environ 137,5° pour l’angle d’or.
Bon, on sait maintenant que suite de Fibonacci et nombre d’or sont liés même si on ne voit pas forcément bien encore le rapport avec le nombre de spirales dans un sens ou dans l’autre.
Imaginons désormais que les feuilles ne s’écartent plus radialement pendant la croissance mais qu’elles poussent les unes au-dessus des autres, sur une même tige. Qu’elles s’écartent verticalement en somme, les deux variables devenant zi et θi . On peut alors lire ci ou là que parmi tous les angles entre deux feuilles successives, l’angle d’or est pile-poil celui permettant un recouvrement minimal afin que tout le monde reçoive sa dose de soleil dans le meilleur des mondes possibles.
On se doute bien que tout angle α diviseur de 360° ou même tel que α/360 soit un nombre rationnel a/b ne sera pas un choix idéal étant donné qu’au bout d’un certain nombre de générations, b pour être exact, la première feuille et la (b+1)ème seront l’une au-dessus de l’autre, la jeunette jetant une ombre cruelle sur son irrespectée aïeule.

Conclusion, un recouvrement minimal correspondra nécessairement à un angle irrationnel. Pas de recouvrement périodique dans ces conditions. Et parmi tous les irrationnels, celui qui sera le moins efficacement approximé par un nombre rationnel sera le meilleur choix. Et devinez quel est ce nombre ? Le nombre d’or bien sûr.
Creusons un peu les approximations pour nous en convaincre. Le but est d’approcher au plus près un nombre irrationnel x par une fraction p/q.
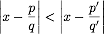
pour tout nombre rationnel p’/q’ différent de p/q avec 0<q’≤q. Aucune fraction de dénominateur plus petit n’approche mieux le nombre x.
Cette définition a un défaut, elle ne nous dit pas si le nombre irrationnel est «facile» à approximer, c’est-à-dire si les valeurs de q vont rapidement devenir énorme ou non. En effet, la «bonne approximation» a un côté artificiel puisque
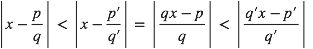
est toujours validé pour des p/q et p’/q’ extrêmement proche du moment que q soit bien plus grand que q’. On se retrouve avec des dénominateurs énormes sans progrès notables dans l’approximation...
Cela nous amène à définir une meilleure approximation, récompensant les dénominateurs plus petits, l’idée étant de multiplier l’écart entre x et p/q par le dénominateur q :
pour tout nombre rationnel p’/q’ différent de p/q avec 0<q’≤q, p/q est la meilleure approximation du réel x si :
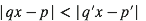
pour tout nombre rationnel p’/q’ différent de p/q avec 0<q’≤q, p/q est la meilleure approximation du réel x si : |qx-p|<|bx-a|.
Avec cette définition, 13/4 qui était une bonne approximation de π (d’après la première définition) n’est plus une meilleure approximation puisque 3/1 lui damne le pion (4π-13 n’est pas inférieur à π-3) et ce bien que 3/1 soit plus éloigné, c’est la prime au petit dénominateur.
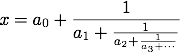
Et on note x = [ a0 ; a1 , a2 , a3 , ... ].
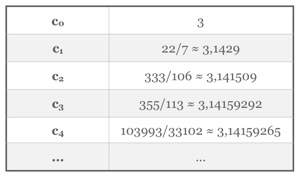
Prenons l’exemple de π :
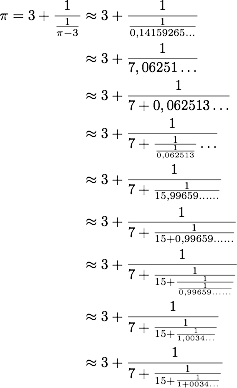
Donc π=[ 3 ; 7 , 15 , 1 , ... ]
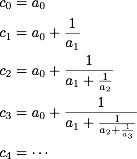
On peut aussi démontrer, et c’est un des principaux attraits des fractions continues, que les réduites d’ordre cn sont chacune les meilleurs approximations d’un nombre réel pour le dénominateur qn.
Pour π, les premières réduites sont :
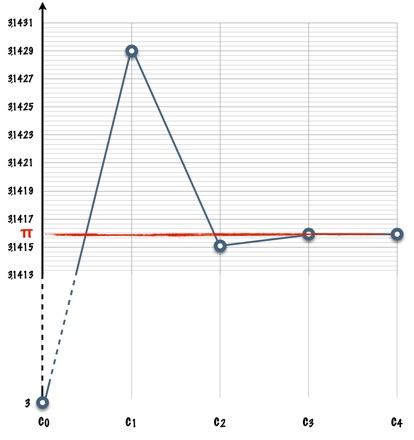
On observe effectivement un rapprochement progressif des réduites, par défaut et par excès alternativement.
Deux autres équations vont nous permettre de conclure.
La première est une relation de récurrence entre les dénominateurs qn des réduites :
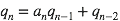
La seconde demande un peu plus de travail (voir ici pour toutes les démos) :
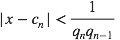
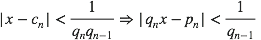
Ce qui montre que plus les qn sont grands et meilleures sont les meilleures approximations.
Or d’après la relation de récurrence sur les qn, des grands qn correspondent à des grands an.
Conclusion : le nombre irrationnel le moins bien approximé, le plus irrationnel en somme, correspondra à la fraction continue ayant les plus petits an. Le pire scénario étant que tous les an valent 1 :
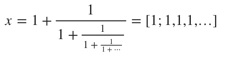
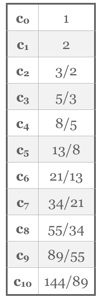
Les premières réduites sont reportées ci-dessous :
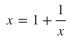
on se retrouve à résoudre le même trinôme que plus haut. x n’est autre que φ, le nombre d’or (ça nous permet, en passant, de confirmer l’assertion du départ :
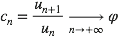
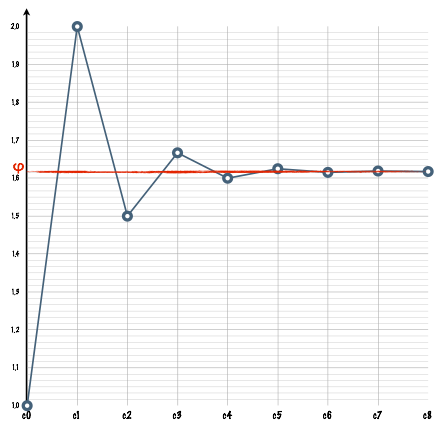
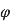
Finalement, on a montré que le nombre d’or est le nombre le plus irrationnel, donc le moins bien approché par une fraction, donc aboutissant à la disposition optimale des feuilles autour d’une tige pour éviter au maximum leur recouvrement !
Cette extraordinaire optimisation témoigne pour les plus angoissés de la main verte d’un grand horloger. Comment la nature pourrait-elle être si bonne en maths ?
Dans ce cas, elle n’en a pas eu besoin, mais elle le peut ! C’est le principe de la sélection naturelle d’aboutir à un optimum si la pression sélective est suffisamment forte. Une série immense d’essais et d’échecs finirait fatalement par accoucher aléatoirement de cette solution optimale qui perdurerait si l’avantage reproductif le permettait.
Mais dans ce cas, nul besoin de tester des millions d’angles. L’angle idéal est choisit automatiquement par un mécanisme ridiculement simple...
On retourne donc à la situation où les feuilles s’écartent radialement et non plus verticalement pendant la croissance de la plante, le cas du tournesol et de la pomme de pain.
Quelque soit l’angle fixe entre deux éléments, deux jeux de spirales se dessinent naturellement. Ils correspondent à l’encadrement de
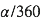
Mais une infinité de réduites encadre x, lesquelles choisir ? Là, ça ne dépend plus que du nombre d’éléments, du niveau de détail en somme. S’il y en a peu, n sera petit et plus on en ajoute, plus la figure grandit et plus les spirales apparentes correspondront à des n élevées (les petits n sont toujours là mais s’entortillent tellement qu’on perd leur trace). Les spirales les plus facilement identifiables ne font pas plus d’1 ou 2 tours, n est choisi en fonction.
Un exemple pour y voir plus clair :
prenons l’angle 161,5°.
La fraction continue de
161,5/360 ≈ 0,4486111... s’écrit [0,2,4,2,1,2,1,5,1] (un «continued fraction» dans Wolfram Alpha fait l’affaire) et la suite des réduites est reportée dans le tableau ci-dessous.
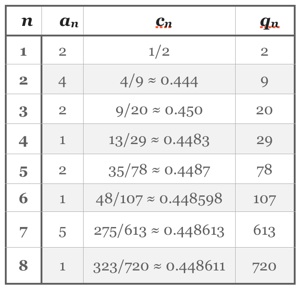
Avec 50 éléments on observe facilement 2 spirales tournant dans un sens et 9 dans l’autre.
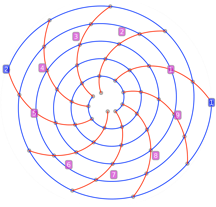
À 100 éléments, la réduite suivante, faite de 20 spirales, devient plus facilement observable que le jeu de 2 spirales.
En passant à 300 éléments, les deux jeux précédents de spirales restent visibles mais les neuf spirales rouges commencent à sacrément s’enrouler...
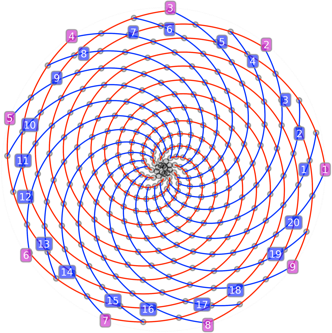
Et de fait, la réduite suivante correspondant à un jeu de 29 spirales pointe le bout de son nez :
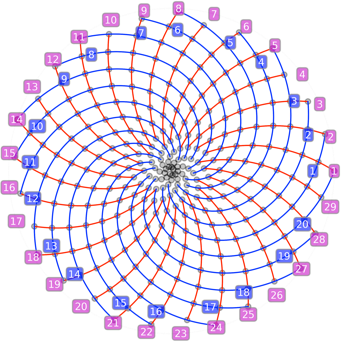
Et avec 1200 éléments, ce sont 78 spirales qui deviennent discernables :
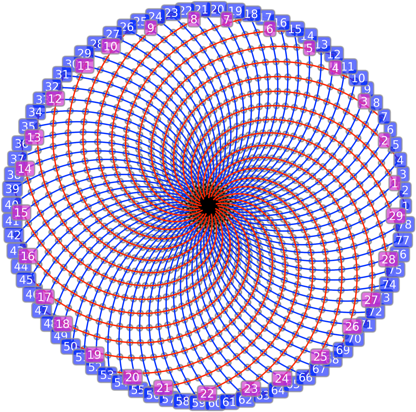
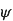
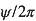
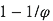
Les nombres de spirales observables, donnés par les dénominateurs qn des réduites, sont donc les termes de la suite de Fibonacci !
Pour des petits nombres d’éléments (de feuilles, écailles, fleurons,...) on est sur les premières réduites (3, 5, 8, 13 spirales) comme pour les pommes de pin, et sur des plantes comme les tournesols, aux fleurons très nombreux, on peut observer jusqu’à 144 spirales.
Il nous reste à comprendre comment l’angle d’or émerge naturellement dans tous ces cas...
Mais avant d’en arriver là, revenons sur l’interprétation de ces figures géométriques.
Ces jeux de spirales ne sont-ils pas une merveilleuse illustration graphique des fractions continues et de leurs réduites ? Ces billes distribuées à angle et augmentation de rayon constant permettent de «voir» la rationalité et l’irrationalité d’un nombre à une certaine approximation près correspondant à un certain niveau de détail, de zoom.
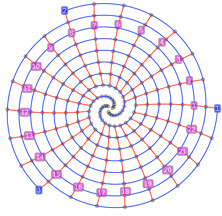
Une valeur rationnel p/q de x se traduit par une périodicité dont l’ordre est donné par le dénominateur q puisque les q premiers éléments auront les mêmes angles que les q suivants et ainsi de suite. Les particules dessinent donc q rayons. Les nombres rationnels sont ainsi tout naturellement visualisés.
Et si on s’écarte un peu de p/q, les rayons commencent à se courber et s’enrouler, c’est la naissance des spirales. Les q éléments suivants ne sont plus alignés avec les q premiers mais un peu décalés et ce décalage augmente à chaque «période». Et plus on s’éloigne de p/q, plus les spirales s’enroulent. On est alors poussé vers une autre meilleure approximation rationnelle dont le jeu de spirales, en sens opposé, se redressent en rayons au fur et à mesure de l’approche.
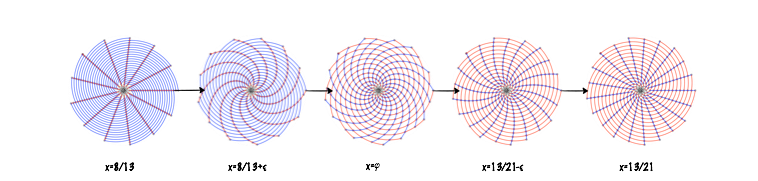
Cette représentation graphique rend aussi plus claire la vitesse de convergence des réduites vers le nombre irrationnel visé.
Dans une fraction continue, des grands an entraînent de grands qn (par construction) et pour que les spirales correspondant à ces imposants dénominateurs deviennent visibles, il faut s’écarter suffisamment, ce qui revient à rajouter de nombreux éléments ou encore à augmenter largement la précision.

Quelques éléments suffisent pour visualiser la première réduite de π alors qu’il en faut plusieurs milliers pour voir se courber nettement les branches de la seconde...
Au contraire, φ, que les rationnels peinent à approcher, présente, à quantité d’éléments fixée, le plus grand nombre de jeux de spirales rencontrés.
Les deux vidéos suivantes permettent de se rendre compte de l’importe différence d'irrationalité entre π (la première) et φ (la seconde).
Et avec 30 000 éléments :
π