fantasmes spiralés
Bon, revenons à l’origine de tout ça. Pourquoi Fibonacci ?
Chaque nouvelle «particule» est créée dans une zone centrale. Et il suffit d’un quelconque mécanisme lui disant d’aller le plus loin possible de ses copines déjà présentes pour que l’affaire soit dans le sac. Que cela soit par une histoire d’encombrement stérique résultant en une pression, de diffusion d’inhibiteur, d’instabilités, le résultat est le même : au bout d’un certain nombre de générations, l’angle le plus loin possible de tous les autres a toutes les chances de converger.
Et si le paramètre clé de cette histoire, à savoir le taux de croissance, la vitesse d’écartement radiale des particules, est suffisamment faible, cet angle sera l’angle d’or !
On peut préciser les choses en se penchant sur l’anatomie de la plante et plus précisément sur l’endroit où chacune des particules apparaît, du doux nom d’apex. La partie active de division cellulaire est composée de différentes zones mais pour ce qui nous intéresse, les futures feuilles (ou autres) que sont nos particules (appelées, elles, primordia) sont créées à la frontière d’une zone circulaire. C’est donc sur ce cercle que l’angle est choisi.
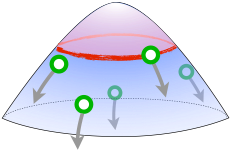
Cela rend les choses très simples à modéliser informatiquement. Il suffit de construire un «potentiel énergétique» dépendant inversement des distances à chaque particule présente
(
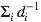
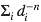
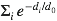
-
•on cherche la valeur minimum du potentiel sur un cercle de rayon r0 en fonction des i-1 particules déjà présentes. Ça nous donne un angle θi.
-
•on créé une nouvelle particule i sur le cercle au minimum trouvé précédemment (r0, θi).
-
•on avance radialement les i particules créés d’une distance drk en gardant leurs directions θk constantes. Pour simplifier encore les choses, on a pris un drk = dr constant (il sera toujours possible de le compliquer par la suite).
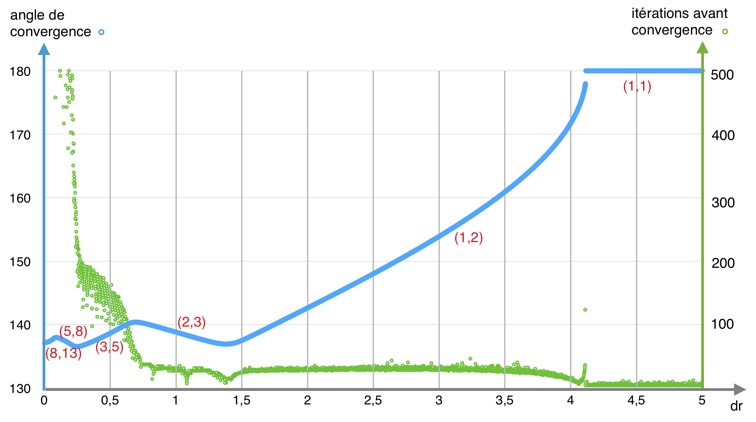
Résultats : dans la plupart des cas (on reviendra là-dessus), l’écart angulaire entre deux particules consécutives, θk - θk-1, converge (encore heureux puisque sans cette convergence, point de spirale) et l’angle obtenu dépend du rayon de la zone centrale où naissent les particules, r0, et de la distance radiale dr entre deux générations.
Plus précisément, pour un potentiel donné, on observe plusieurs étapes au fur et à mesure de la diminution de dr ou plutôt du paramètre adimensionné dr/r0.
-
1.Le calme plat
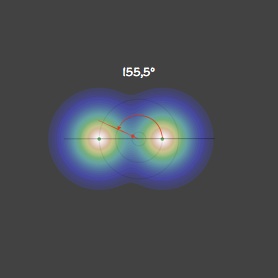
Pour un dr suffisamment grand, la situation est simple, chaque particule nait diamétralement opposé à la précédente.




2. La brisure
En-dessous d’un certain seuil pour dr/r0 (dépendant du potentiel), l’influence de la particule de génération i-2 devient suffisante pour écarter la nouvelle née de l’axe horizontal qu’elle occupait jusqu’ici, faisant passer l’écart θ2 - θ1 sous les 180°, dans un sens ou dans un autre. L’ancien minimum est remplacé par deux minima symétriques par rapport à l’axe horizontal. Le choix de l’un des deux berceaux brise la symétrie originelle.
On est confronté ici à un cas typique de flambage ou plutôt une bifurcation «de fourche» supercritique dans le jargon.
L’analyse de ce type de bifurcation repose toujours sur les mêmes ingrédients : l’approche de la deuxième particule se traduit par l’influence grandissante d’un terme d’ordre 4 dans le potentiel en plus du douillet puits parabolique qui accompagne toute position d’équilibre stable :
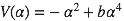
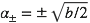
La progression en racine carré de la position d’équilibre signe les bifurcations fourche.
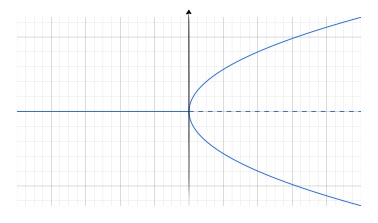
Le basculement sur l’une des deux solutions détermine le premier sens d’enroulement des spirales.
Quelque soit la disposition des premières générations ou même si l’angle d’une des particules est modifié accidentellement, l’angle θk - θk-1 entre deux particules consécutives tend vers une valeur stable ne dépendant que de dr/r0. En effet, la suite récurrente des θk (θk = f({θj<k}) tend vers un point fixe attractif.
On peut s’en convaincre en traçant l’angle correspondant à la position où nait la particule de 3ème génération, sur le cercle central, en fonction de l’angle de la 1ère génération en gardant la seconde fixe. On couvre alors toutes les configurations pour les deux premières particules et tant que dr/r0 n’est pas trop petit (voir le troisième point de notre discussion) la présence de générations antérieures ne change quasiment rien à l’histoire (faible influence).
dr/r0 sous le seuil
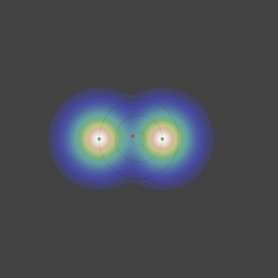
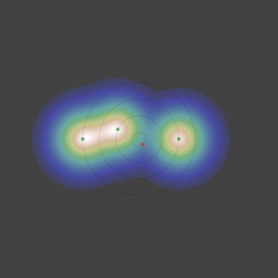
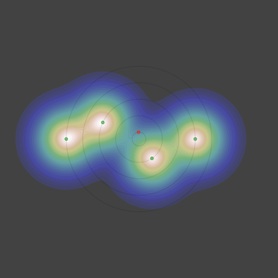
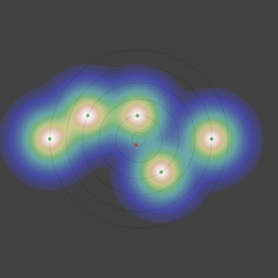
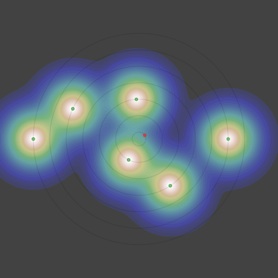
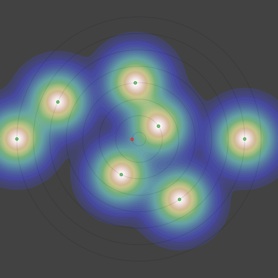
vu par la dernière génération
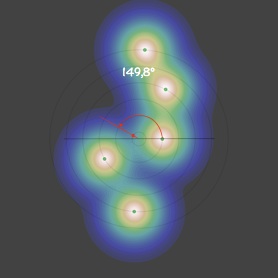
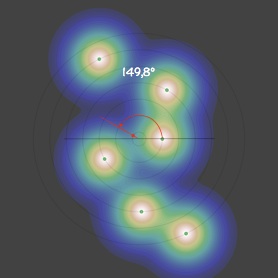
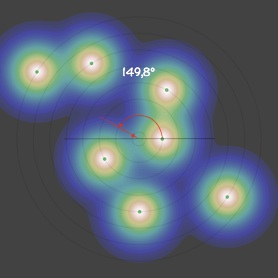
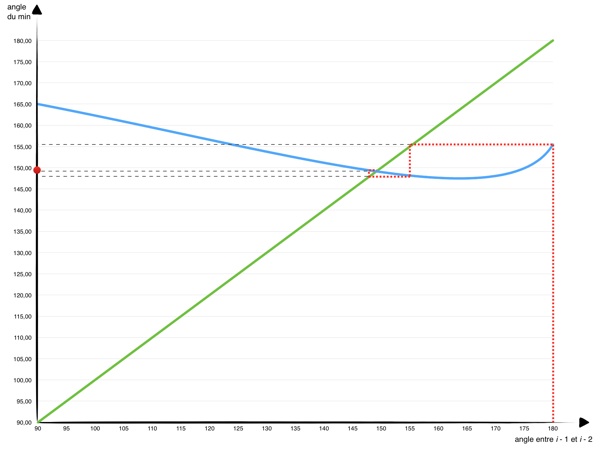
Et que remarque-t-on ? Comme on pouvait s’y attendre la courbe de l’angle minimum ne croise la première bissectrice qu’une seule fois et décroit alors «gentiment», avec une pente inférieure à 1, ce qui rend le point fixe (f(θ) = θ) attractif.
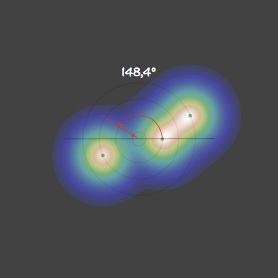
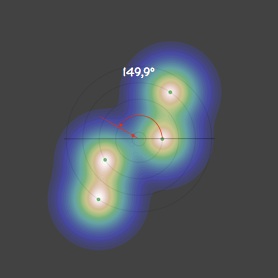
Avec θ1 = 180°, on reproduit à peu près les diapositives précédentes : θ2 ≈ 155,5°, θ3 ≈ 148,1°, θ4 ≈ 149,4°, θk>4 ≈ 149,1°. La petite différence d’un peu moins d’1° s’expliquant par l’influence des générations antérieures, non prise en compte pour l’établissement du graphe (i-3, la plus proche, va avoir tendance a pousser le minimum vers i-2 ce qui va dans le sens de l’écart relevé).
Plus dr se réduit et plus la grand-mère i-2 repousse la dernière née et donc, dans un premier temps, l’angle fixe entre deux générations ne fait que diminuer.
-
3. Les rebroussements
On continue de rapprocher les générations et de fait, l’influence des générations antérieures se fait de plus en plus sentir.
Première conséquence, la convergence vers un angle fixe demande plus d’étapes, jusqu’à ce que le coeur ne soit plus perturbé par les premières nées.
Autre conséquence, plus spectaculaire, le secours portée par l’arrière-grand-mère i-3 à la mère i-1 pour contrecarrer l’influence de la grand-mère i-2 finit par porter ses fruits. L’angle cesse de diminuer et finit même, quand i-3 est suffisamment proche, par rebrousser chemin.
L’angle augmente alors jusqu’à ce que i-2 reçoive à son tour une aide notable, celle de i-5. Plus dr/r0 diminue et plus l’influence de i-5 grandit et permet de renverser à nouveau l’évolution de l’angle...
Et si on trace l’évolution de l’angle entre deux particules successives (sous-entendu la valeur vers laquelle cet angle converge) en fonction de dr/r0, on observe bien, une fois la première rupture de symétrie passée, une alternance de phases croissantes et décroissantes, de plus en plus rapides. Et l’enchaînement de ces branches conduit vers l’angle d’or.
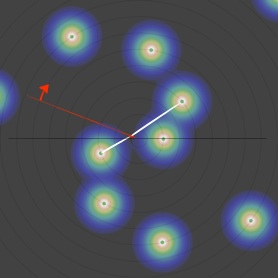
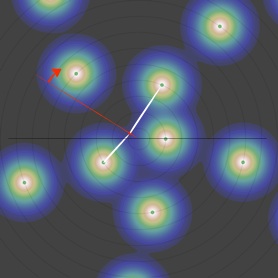
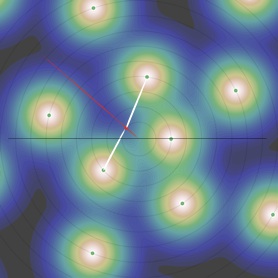
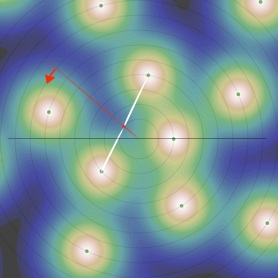
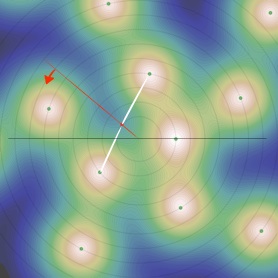
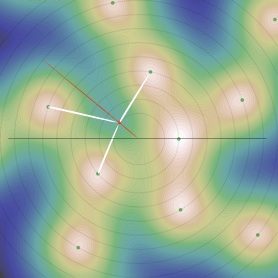
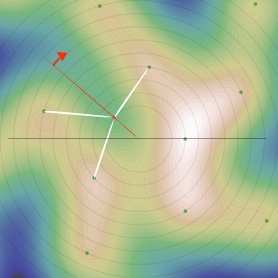
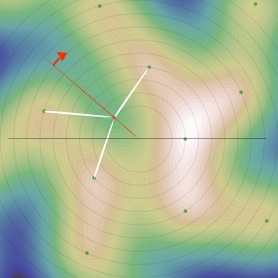
Reparlons un peu des spirales :
-
•Pour dr/r0 grand, il n’y en a pas. L’influence de i-1 est la seule à prendre en compte à chaque tour. L’angle reste constant et on appelle cette branche horizontale (1,1). Chaque nombre désigne la spirale, c’est-à-dire la périodicité à laquelle appartienne les deux particules influençant majoritairement la position du minimum.
-
•Quand dr/r0 passe sous le seuil de brisure de symétrie, l’angle commence sa chute et les spirales apparaissent, une de chaque côté, correspondant à l’influence d’intensité comparable de i-1 et i-2. La dernière née apparaît entre elles, plus proche de 2 mais s’en éloignant progressivement. Cette branche est (1,2).
-
•Au premier rebroussement, c’est l’influence comparable de i-2 et i-3 qui détermine la position du minimum. Il naît donc entre la spirale formée des particules {i-2, i-4, i-6, i-8,... } et celle formée de
{i-3, i-6, i-9, i-12,...}. La spirale de périodicité 1 (difficilement visualisée comme une spirale) est donc remplacée par la spirale de période 3, ce qui donne une branche (2,3). -
•Au second rebroussement, c’est la spirale de période 2 qui est remplacée par la spirale de périodicité 5, d’où (3,5).
r0 = 2 et potentiel en e-d/0,1
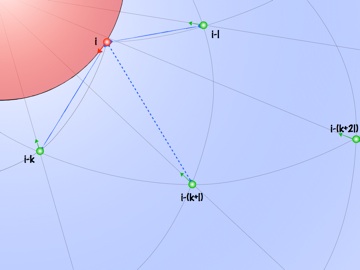
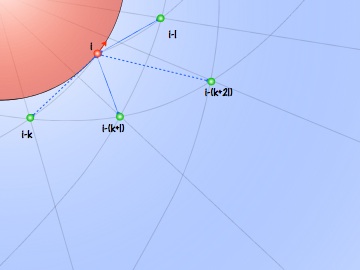
Supposons que le dernier rebroussement soit dû à l’influence principale des particules i-k et i-l avec k<l. La nouvelle particule apparaît donc entre un jeu de spirale de périodicité k et un autre de périodicité l et est poussée, après le rebroussement, de l vers k puisque l est plus vieille donc au départ moins influente ; son rapprochement s’oppose à l’influence antérieure de k.
À qui k va-t-elle passer le relai ? À l+k pardi ! Les deux spirales sont courbées l’une vers l’autre et donc se croisent au-dessus du dernier rejeton. Par construction, la particule appartenant à ce croisement est l+k. C’est elle qui va rapidement s’opposer à l’influence de l (elle s’approche plus vite puisqu’elle est plus loin, une diminution δdr la rapproche de (l+k)δdr).
On peut se convaincre de la nouvelle périodicité l+k en oubliant la répulsion des particules plus vieilles que l. Seuls les deux jeux de spirales de périodicité l et k se repoussent maintenant. Si on fait tendre dr vers zéro, les spirales se redressent en l+k rayons entre lesquels naissent les nouvelles particules avec, du coup, cette même périodicité correspondant à la somme des deux anciennes.
Mais si on rebranche la répulsion des ancêtres, plus moyen d’en arriver là, la position de la nouvelle particule i va rebondir avant d’atteindre l’angle correspondant à la périodicité l+k, éjectée par i-(l+k) en personne.
Et ensuite ? C’est le même raisonnement ; les deux spirales encadrant la future particule sont maintenant l et l+k et leur premier croisement correspond à 2l+k qui va repousser à son tour la position du minimum avant que l’angle correspondant à sa périodicité (2l+k) soit atteint, etc.
La position de la dernière particule ne fait donc que rebondir, quand dr/r0 diminue, entre des jeux de spirales de plus en plus rapprochées k, l, k+l, k+2l, 2k+3l, etc.
Les périodicités des branches successives sont liées comme un+2 = un + un+1. Et oui, comme Fibonacci. Ajoutons à cela qu’on a commencé avec u1 = 1 et u2 = 1 et on se retrouve bien avec la célèbre suite : 1, 1, 2, 3, 5, 8, 13, 21, etc.
Or c’est la périodicité des spirales entre lesquelles naissent les dernières particules que l’on vient de déterminer. Périodicité de spirales correspondant à des angles rationnels de dénominateurs qn = 1, 1, 2, 3, 5, 8, 13, 21, etc.
La position de la dernière particule est donc repoussée entre les meilleures approximations successives de l’angle d’or, chacun de ces rationnels la forçant l’une après l’autre vers l’irrationnel qu’ils encadrent.
Ou dit autrement, l’angle de la dernière particule est petit à petit comprimé par deux réduites consécutives de ψ dont l’ordre et donc la proximité augmente quand dr/r0 diminue (puisque c’est cette diminution qui fait passer d’un jeu de spirales à l’autre, d’une réduite à la suivante). Et par conséquent, comme les réduites, l’angle tend vers ψ.
Et pour finir sur ces spirales, la vidéo qui suit montre l’évolution de la disposition des particules avec la diminution de dr (les rayons sont artificiellement gardés constants pour la visualisation).
r0=2, N=200
rouge : i
orange : i-1
jaune : i-2
vert : i-3
bleu clair : i-5
violet : i-8
fuchsia : i-13
rose : i-21
Conclusion : des spirales possédant une périodicité correspondant à deux nombres consécutifs de la suite de Fibonacci ont toutes les chances de se retrouver couramment.
À une condition néanmoins : les rebonds suivent Fibonacci seulement si on commence sur la branche (1,1). Un dr/r0 faible fixé dès le départ peut tout à fait aboutir à un autre angle irrationnel cible que l’angle d’or.
En effet, d’autres minima, correspondant à d’autres branches, coexistent mais il ne sont pas connectés continûment à la branche (1,1). Seules les branches convergeant vers l’angle d’or ont ce privilège.
Par conséquent, dans les plantes présentant une structure spiralée de type Fibonacci, on peut supposer que la croissance débute par un régime transitoire correspondant à une forte vitesse d’écartement ou un important délai entre deux primordia (on peut écrire dr = vΔt produit de la vitesse de croissance par la durée entre deux générations) avant de converger vers une faible valeur. On s’assurerait ainsi de l’accroche vers l’angle d’or.