Expérience 1 : capacité thermique massique de l’eau
dans un calorimètre supposé idéal, on chauffe une certaine masse d’eau (200 g, 300 g ou 400 g) grâce à une résistance électrique (R = 0,50 Ω) sous une tension de 6,0 V.
La puissance fournie à l’eau vaut alors P = U×I = U²/R = 72 W
et l’énergie apportée vaut ΔE = P×Δt = 72×Δt.
Si on trace l’énergie apportée ΔE = P×Δt en fonction de l’élévation de température Δθ,
on obtient les 3 graphes suivants :

On remarque donc que l’énergie apportée et l’élévation de température sont proportionnelles :
ΔE = C×Δθ où C est appelée capacité thermique. C est d’autant plus grande que la masse d’eau est grande, mais c = C/m, la capacité thermique massique (en J.K-1.kg-1) est, elle, indépendante de la masse et vaut, pour l’eau : ceau = 4,18.10³ J.K-1.kg-1. On a alors :
ΔE = m×c×Δθ
capacité thermique du calorimètre
Un calorimètre réel a lui aussi une certaine capacité thermique (la plus faible possible).
Connaissant celle de l’eau, on peut calculer celle du calorimètre.
Avec un calorimètre réel, il faut Δt = 246 s pour faire passer m = 200 g d’eau de θ₀ = 20°C à θ₁ = 42°C.
Que vaut alors Ccalo, la capacité thermique du calorimètre utilisé (on néglige les pertes énergétiques) :
Si on néglige les pertes, toute l’énergie apportée est distribuée à l’eau et au calorimètre et comme l’eau et le calorimètre restent en contact, on peut supposer que leurs températures sont les mêmes (équilibre thermique) :


On aurait aussi pu déterminer la capacité thermique du calorimètre autrement : supposons qu’il contienne initialement m1 = 200 g d’eau et que cette eau et le calorimètre soit à l’équilibre thermique à une température θ1 = 20°C. On ajoute alors une masse m2 = 200 g d’eau à θ2 = 40°C. On attend que le nouvel équilibre thermique se fasse ; la température finale se stabilise à θf = 29,7°C. Que vaut Ccalo ?
Expérience 2 : déterminer la capacité thermique de différents matériaux
dans un calorimètre sans perte énergétique et de capacité thermique C contenant 300 g d’eau (θ₀ = 20°C), on place un morceau de brique de 325 g ou un morceau d’acier de 400 g préalablement chauffés à θ₁ = 100°C (dans de l’eau bouillante). Grâce à l’élévation de température mesurée, on peut déterminer les capacités thermiques massiques de la brique ou de l’acier.
Il n’y a maintenant plus d’énergie apportée par l’extérieur mais seulement une mise à l’équilibre thermique entre l’eau + calorimètre et le morceau de brique ou d’acier. Le corps chaud (brique ou acier) perd de l’énergie thermique et le corps froid (eau + calorimètre) en gagne :
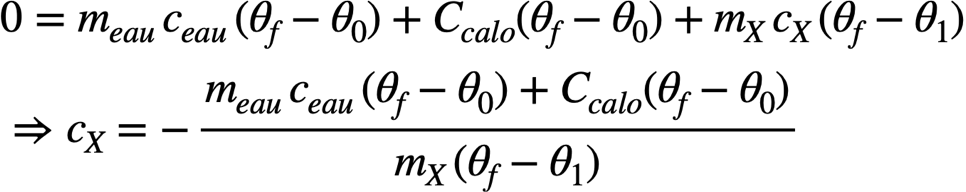
Pour la brique, mX = 0,325 kg et θf = 34°C ; on obtient alors cX = 0,85 kJ.K-1.kg-1
Pour l’acier, mX = 0,400 kg et θf = 30°C ; on obtient alors cX = 0,47 kJ.K-1.kg-1
Conclusion : à masse égale, la brique peut emmagasiner presque deux fois plus d’énergie thermique que l’acier pour une même élévation de température.
Petit programme Python pour calculer la température finale atteinte lorsqu’on place ensemble deux corps de températures diffrérentes :
On place un seau de 5 L d’eau chaude (T1 = 70°C) dans une salle cubique initialement à une température T2 = 20°C.
Si on néglige toute perte thermique par les parois de la salle et tout renouvellement d’air, que vaut la température finale Tf à l’équilibre thermique ?
données :
ceau = 4,18 kJ.kg-1.K-1
cair = 1,00 kJ.kg-1.K-1
ρeau = 1,0.103 kg.m-3
ρair = 1,2 kg.m-3