-
 Cylindre :
Cylindre :
Ecoulement uniforme de vitesse U perturbé par un cylindre de rayon R et d’axe perpendiculaire à l’axe des vitesses (⇒pb à 2D).
Pour trouver la solution de l’équation de Laplace correspondant à cet écoulement, on va superposer un écoulement permanent à un développement multipolaire autour du cylindre jusqu’à ce que la solution respecte les conditions aux limites de la situation. Le développement multipolaire est le développement en série de la partie du potentiel décroissant avec la distance.
Expliquons cela : loin de l’obstacle, sa présence ne se fait plus sentir et donc son potentiel est de la forme f(r)g(1/lr-r0l) (en supposant qu’il soit centré en r0), où f(r) prend en compte la forme de l’obstacle. On peut développer g(1/lr-r0l ) en série de Taylor et approximer le résultat en s’arrêtant à un ordre donné. Le développement en série de g(1/lr-r0l) est ce qu’on appelle un développement multipolaire. En effet, chaque puissance (négative) successive du développement correspond à l’addition d’un potentiel créé par un multipôle de nombre de pôles croissant (dipôle, quadrupôle, octopôle,...). Le potentiel d’un dipôle est bien par construction la différence entre 2 potentiels monopolaires très proches, c’est donc une dérivée spatiale du potentiel du monopole. De même, le potentiel du quadripôle est la différence entre 2 potentiel dipolaires très proches, etc...
Dans le cas du cylindre, pas besoin de chercher très loin... Le terme dipolaire est la solution exacte au problème (la représentation du champ de vecteur dipolaire “vu de loin” permet de se convaincre que cela peut suffire). Arrêtons donc le développement de g au premier terme :
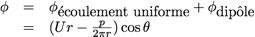
On en déduit :
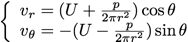
Reste à vérifier s’il existe une valeur de p telle que ce champ de vitesse vérifie les conditions aux limites :
1) v=U à l’infini → pas de problème, ∀ p
2) vr(r=R)=0 (on ne rentre pas dans le cylindre) → condition sur p :
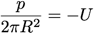
d’où :
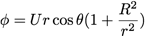
et finalement :
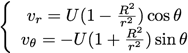
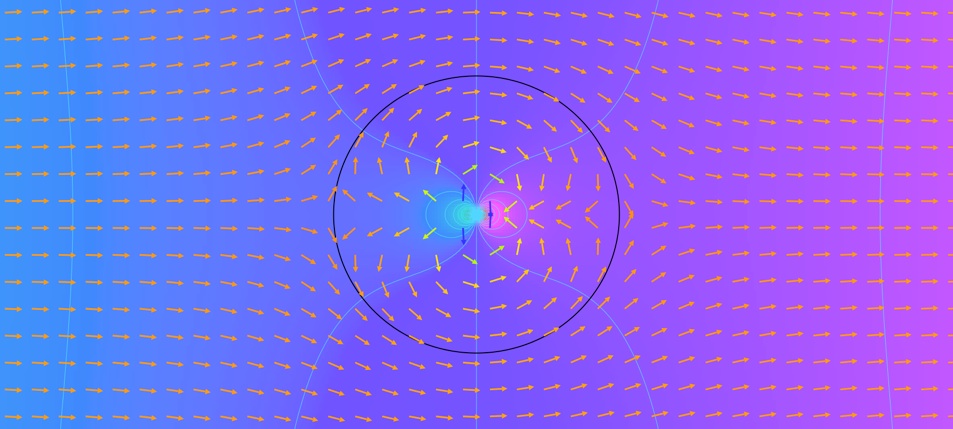

On obtient pour la fonction courant :
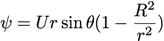
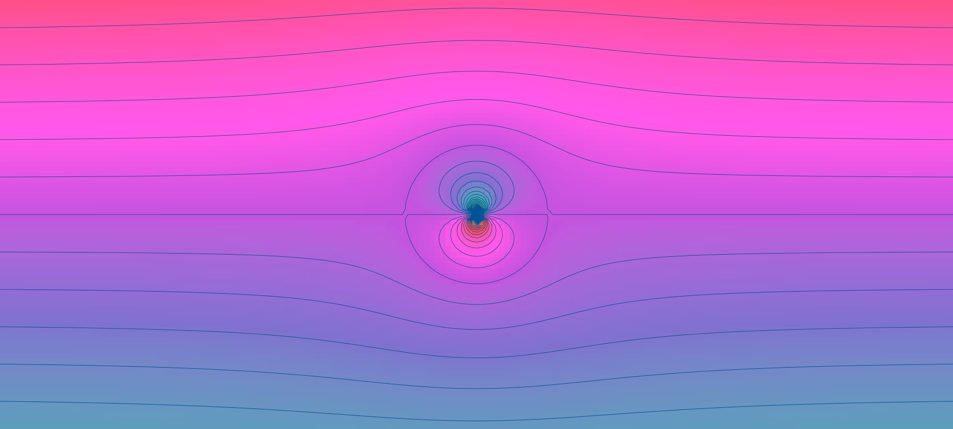
r=R et θ=0 ou π sont des points d’arrêt (vitesse nulle)