Pas à pas simple pour établir la matrice de transformation de Lorentz
source : «Relativity made relatively easy» de Andrew M. Steane

On cherche à relier les coordonnées (t, x, y, z) d’un référentiel R aux coordonnées
(t’, x’, y’, z’) d’un deuxième référentiel R’ en translation rectiligne uniforme par rapport au premier, à la vitesse v, parallèlement à l’axe des x.
Les axes correspondants sont alignés et on fait coïncider les origines spatiales de chacun des référentiels à t=t’=0.

On part de l’hypothèse, validable à posteriori, que la transformation liant ces deux jeux de coordonnées est linéaire.
On peut donc écrire :

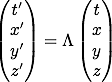
Où Λ est une matrice 4×4.
16 termes à trouver... mais armé du principe de relativité et de l’invariance de la vitesse de la lumière, on va s’en sortir sans trop de difficultés.

Première étape :

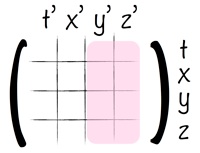
On a nécessairement y’=y et z’=z !
On peut s’en convaincre en prenant deux cylindres rouge et bleu de mêmes dimensions qu’on envoie l’un vers l’autre.
Dans l’hypothèse où les coordonnées transverses sont modifiées, le rayon du cylindre en mouvement change par rapport à celui à l’arrêt, disons par exemple qu’il rapetisse. Dans le réferentiel du cylindre bleu, seul le cylindre rouge est en mouvement. On doit se retrouver alors avec un cylindre rouge passant à l’intérieur du cylindre bleu.

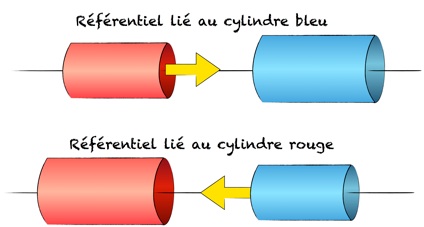
Mais vu du cylindre rouge, c’est le bleu qui bouge et on s’attend donc, dans ce référentiel, à un rayon bleu diminué. Sans cela, le principe de relativité en prendrait un coup... Dans le référentiel du rouge, c’est donc le cylindre bleu qui passe à l’intérieur de l’autre.
Les deux situations sont difficilement compatibles ! Le seul moyen de réconcilier les points de vue est de garder des dimensions transverses constantes pendant le mouvement.

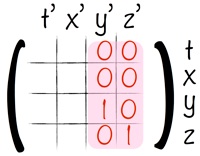
Deuxième étape :

C’est le moment délicat car on doit s’attarder un peu sur la notion de simultanéité en relativité restreinte.

Considérons une particule se déplaçant dans la direction x à la vitesse v constante par rapport à R. Sa ligne d’univers (ie sa trajectoire dans l’espace-temps) est donc une droite de type temps de pente supérieure à un (on prend  c=1 pour simplifier et avoir un cône de lumière à 45°).
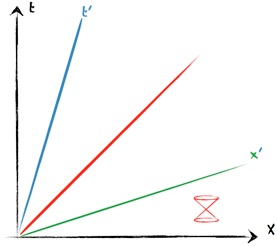
La ligne d’univers de la particule mesure son temps propre t’. Rappelons en effet que le temps propre d’un mobile se mesure à cheval sur le mobile en regardant sa montre, ce qui revient à mesurer la longueur de sa trajectoire dans un diagramme d’espace-temps.
Des évènements seront alors perçus comme simultanés pour la particule en mouvement si et seulement si ils sont enregistrés au même instant propre t’.

Un des moyens à la disposition de la particule pour connaître la date d’un évènement est l’écho radar : elle balance un photon en t’1 et le reçoit après rebond en t’2. L’invariance de c lui assure que l’évènement «le photon rencontre l’obstacle» s’est déroulé à (t’1 + t’2)/2.
Mais il n’y a pas qu’un seul évènement pouvant être enregistré à cet instant ; tous ceux  dessinant l’axe vert seront perçus comme simultanés pour la particule !
Si on change l’abscisse x où l’instant t de l’évènement, il sera vu à un instant t’ différent, montrant la dépendance t’ envers t et x, à moins que la variation ne se fasse le long de l’axe de simultanéité, ce qui lie alors nécessairement les 2 variations Δx et Δt.

Rq : la ligne de simultanéité est par définition un axe de type espace pour la particule.

Mais qu’en est-il d’un déplacement de l’évènement selon les y ou les z ? Avec notre méthode d’écholocation, on se rend vite à l’évidence que tout axe perpendiculaire au plan (t, x) est un axe de simultanéité impliquant l’indépendance de t’ vis-à-vis des y ou des z.
En effet, dans un plan (t, y) ou (t, z), les axes t et t’ sont confondus (puisque la vitesse de la particule est nulle dans ces directions). Ainsi, quelque soit la coordonnées yC du point sur le schéma, l’instant t’ sera le même.

t’ ne dépend donc que de x et t (la direction des différents axes suffisait pour nous en convaincre).

Enfin, pour x’, il suffit de récapituler : t’ appartient au plan (t,x) et les axes y’ et z’ restent alignés avec y et z. Par conséquent, x’ ne peut lui aussi que se trouver coincer dans le plan (t,x).
L’axe spatial vert découvert plus haut donne bien la direction de x’.
Et au final, le déplacement a tourné l’hyperplan de simultanéité (x, y, z) dans le plan (t, x).

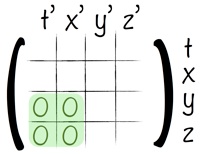
Troisième et dernière étape :

On se retrouve avec le sous-problème :

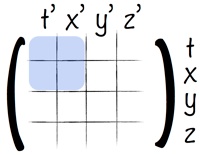
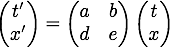
Comme R’ se déplace à v selon x par rapport à R, le points x’=0 est repéré dans R par
x = vt
Et donc 0 = dt + evt ⇒  d = -ev

Et de même, le point x = 0 de R bouge dans R’ en x’ = -vt’ ce qui donne :
-vt’ = dt quand t’ = at ⇒  d = -av

Par conséquent : a = e

Utilisons dans un deuxième temps l’invariance de la vitesse de la lumière :
x = ct doit donner x’ = ct’ :

Et donc : d = bc2

Jusque là, notre matrice 2×2 ressemble à :

Reste à trouver a...

Suffit d’utiliser le principe de relativité ! La transformation de (x, t) à (x’, t’) doit être la même que celle de (x’, t’) à (x, t) avec un v qui devient -v.

Il suffit donc :

1. •d’inverser la matrice précédente :
   

   

   
   
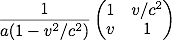
2. •de changer v en -v :
   

   

   
   

3. •et d’identifier à la première matrice.
   

Ça donne :

et donc

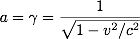
On aboutit finalement à :

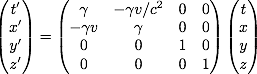
Victoire, on a validé notre hypothèse originelle ; il existe bien une transformation linéaire obéissant à nos impératifs entre les deux référentiels.