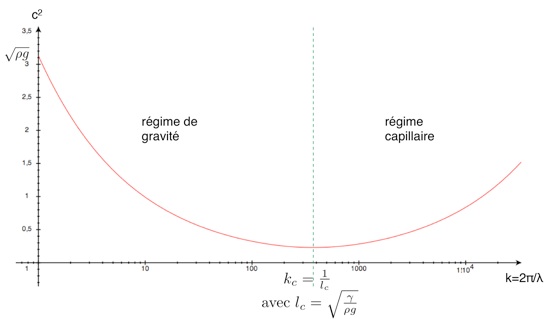
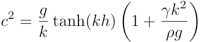Equation de dispersion des ondes de surface
Tiré de Hydrodynamique physique de étienne Guyon, Jean-Pierre Hulin et Luc Petit, EDP sciences/CNRS Editions`
 Les propriétés des ondes se propageant à la surface d’un liquide s’obtiennent en déterminant d’abord le potentiel bidimensionnel qui les caractérise puis en utilisant les lois de la dynamique à la surface (avec les forces de Laplace, de gravité et de pression).
Les propriétés des ondes se propageant à la surface d’un liquide s’obtiennent en déterminant d’abord le potentiel bidimensionnel qui les caractérise puis en utilisant les lois de la dynamique à la surface (avec les forces de Laplace, de gravité et de pression).
On suppose un écoulement irrotationnel, cela nous assure l’existence d’un potentiel bidimensionnel ϕ(x,y,t). Et on le suppose aussi incompressible, ce qui nous indique que le potentiel cherché est solution de l’équation de Laplace : Δϕ=0.
On a la chance de connaître la solution expérimentalement et ça va nous aiguiller dans la résolution de l’équation : on cherche des ondes progressives de faibles amplitudes.

On suppose un écoulement irrotationnel, cela nous assure l’existence d’un potentiel bidimensionnel ϕ(x,y,t). Et on le suppose aussi incompressible, ce qui nous indique que le potentiel cherché est solution de l’équation de Laplace : Δϕ=0.
On a la chance de connaître la solution expérimentalement et ça va nous aiguiller dans la résolution de l’équation : on cherche des ondes progressives de faibles amplitudes.
Tout d’abord, pour résoudre l’équation de Laplace, on va utiliser la méthode de séparation des variables avec comme variable : u=x-ct puisque l’onde doit se propager et y. D’où :`
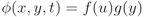
En reportant dans Laplace, on obtient :
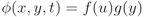
En reportant dans Laplace, on obtient :
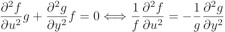
Les 2 membres de l’équation de droite doivent être séparément constants puisqu’ils dépendent de variables indépendantes.
On a donc :
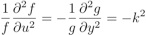
On choisit cette constante puisqu’on cherche une solution sinusoïdale pour f.
On a donc :
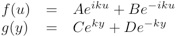
On prend B=0 car on cherche une solution progressive dans le sens des x croissant.
D’autre part, En y=0, la vitesse normale à la surface est nulle :
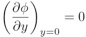
Cela donne :
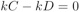
On a donc :
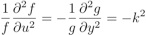
On choisit cette constante puisqu’on cherche une solution sinusoïdale pour f.
On a donc :
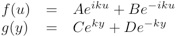
On prend B=0 car on cherche une solution progressive dans le sens des x croissant.
D’autre part, En y=0, la vitesse normale à la surface est nulle :
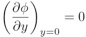
Cela donne :
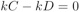
d’où :
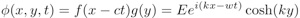
On va maintenant s’intéresser à la dynamique du fluide. Dans l’équation de mouvement, on va négliger le terme inertiel (v.grad)v en supposant que les variations spatiales des vitesses sont négligeables face aux variation temporelles (amplitude de l’onde assez faible). D’où :
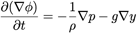
Et après intégration spatiale, on a l’équation de Bernoulli suivante :
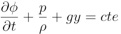
Dérivons-la par rapport au temps :
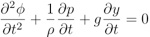
La pression à la surface est donné par la relation de Laplace (qui exprime le lien entre cohésion de la surface et courbure) :
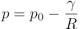
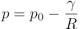
avec
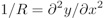
d’où
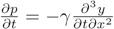
En le replaçant dans l’équation précédente, on obtient :
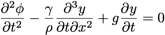
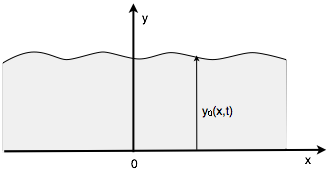
En appelant y0(x,t) la surface libre de l’eau, on a au premier ordre :
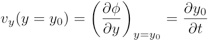
(au premier ordre car on passe d’une dérivée lagrangienne à une dérivée eulerienne)
Plus proprement :
admettons qu’une particule de fluide à la surface y reste :
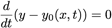
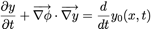
et avec
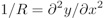
d’où
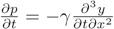
En le replaçant dans l’équation précédente, on obtient :
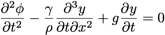
En appelant y0(x,t) la surface libre de l’eau, on a au premier ordre :
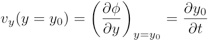
(au premier ordre car on passe d’une dérivée lagrangienne à une dérivée eulerienne)
Plus proprement :
admettons qu’une particule de fluide à la surface y reste :
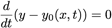
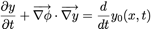
et avec
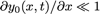
on a finalement :
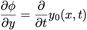
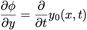
Donc en évaluant notre équation en y0 :
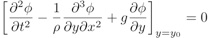
En remplaçant ϕ, on obtient :
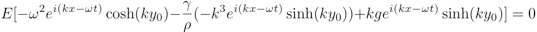
Comme E ne peut être nul, l’expression entre crochet l’est et si on remplace y0 par sa valeur moyenne h, on obtient la relation de dispersion :
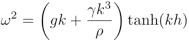
d’où, avec c=ω/k (pulsation temporelle sur pulsation spatiale)
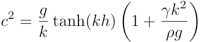
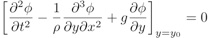
En remplaçant ϕ, on obtient :
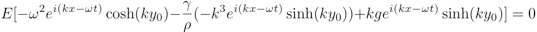
Comme E ne peut être nul, l’expression entre crochet l’est et si on remplace y0 par sa valeur moyenne h, on obtient la relation de dispersion :
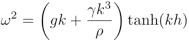
d’où, avec c=ω/k (pulsation temporelle sur pulsation spatiale)