Pages inspirées très fortement du fabuleux «Quantum Field Theory in a Nutshell» de Zee.

Préambule

La théorie quantique des champs née au carrefour entre théorie quantique et relativité restreinte. C’est au point de rencontre de ces deux théories que se comprend enfin un phénomène passionnant : la naissance et la mort de particules ! Le formalisme quantique seul décrit bien l’évolution d’une particule mais, du fait de l’unicité des opérateurs, condamne une particule à vivre éternellement... Mais associée à la relativité restreinte et sa célèbre équivalence entre énergie et matière, la quantique peut enfin voire naître et mourir de nouvelles particules pour des énergies suffisantes.

C’est le formalisme des champs qui a permis cette union et on peut le comprendre classiquement :

prenons un matelas fait de masselottes reliés par des ressorts. Et supposons que la seule variable soit le déplacement vertical qa(t) de chaque masselotte a. Le lagrangien du système s’écrit :

Dans l’approximation harmonique (en ne gardant que les termes quadratiques en q), et en supposant que les q oscillent à la fréquence ω on a l’équation du mouvement de l’oscillateur harmonique avec des modes propres et fréquence propres (venant de la diagonalisation de la matrice kab). On peut alors former des paquets d’onde en superposant les modes propres et quand on quantifie la théorie, ces paquets d’onde se comportent en particules (de la même façon que les paquets d’ondes de l’électromagnétisme, une fois quantifiés, se comportent comme des particules appelées photons).

Comme la théorie est jusque-là, deux paquets d’onde ne peuvent interagir (ils se traversent sans se voir). Par contre, si on inclue les termes non linéaires (cubiques, quartiques, etc...), la théorie devient anharmonique. Les modes propres peuvent maintenant se coupler, les paquets d’ondes interagissent en se rencontrant et peuvent créer de nouveaux paquets d’ondes, un paquet d’onde peut aussi se désintégrer en plusieurs autres, etc... On commence à comprendre pourquoi ce formalisme est particulièrement adapté à la description de la physique des particules...

Mais la théorie des champs n’est pas seulement utile à la physique des hautes énergies et on la retrouve aujourd’hui massivement dans la physique de la matière condensée alors qu’on est plutôt loin de la vitesse de la lumière...

On a vu que la complexité, la richesse, naissait de la prise en compte des termes non harmoniques dans le Lagrangien. Or toute une classe de phénomènes peut faire intervenir de tels termes dans le Lagrangien : il suffit que la corrélation entre voisins soit forte, donc qu’elle s’étende au-delà des plus proches. En physique des particules, c’est la portée de l’interaction qui joue le rôle d’une corrélation à longue portée. Dans les cristaux, la corrélation à longue portée des atomes au sein du réseau fait naître les phonons. Et près d’une transition de phase, c’est la propagation d’une fluctuation thermique (par exemple) qui se fait à grande échelle. Donc le formalisme de la théorie quantique des champs va s’appliquer avec succès à l’étude des transitions de phase bien qu’elles n’ont à voir ni avec la quantique, ni avec la relativité restreinte !

Les intégrales de chemin

Parmi les différents formalismes de la quantique, c’est dans celui des intégrales chemin que s’intègre le plus naturellement la théorie des champs.

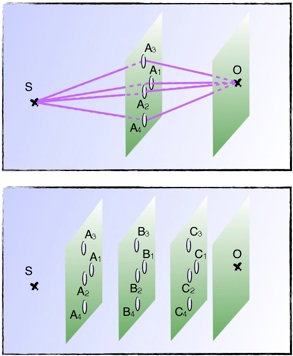
Dans le cas de l’expérience des trous d’Young, la physique quantique nous apprend que l’amplitude pour une particule d’être détecté en un point d’un écran à l’instant T est la somme des amplitudes correspondant à la propagation de S à O par A1 et de S à O par A2.

Imaginons que l’on fasse une infinité de trous dans l’écran, on a maintenant :

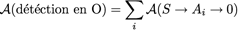
Or quelle est la différence entre le vide et une infinité de trous ?

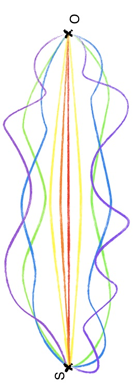
On peut aussi intercaler entre S et O une infinité d’écrans infiniment troués. Et au final, l’amplitude de détection en O à l’instant T d’une particule quantique émise en S, dans un espace vide, est la somme des amplitudes sur toutes les trajectoires possibles (tous le chemins) entre S et O !

En quantique, on ne se déplace pas d’un point à un autre sur une trajectoire précise mais sur toutes les trajectoires possibles...

Partons maintenant de ce qu’on connaît de la mécanique quantique et voyons où cette histoire d’écrans troués nous mène :

Appelons q les coordonnées d’espace (pour éviter des confusions plus loin).

En mécanique quantique, l’amplitude de probabilité de se trouver dans l’état qF (= à la coordonnée spatiale qF) en partant de qI (propagation de qI à qF), en un temps T est donné par l’opérateur unitaire e-iHT, où H est l’Hamiltonien (on peut voir ça comme un postulat pour notre théorie).

En notation de dirac, ça nous donne pour l’amplitude :

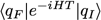
Au lieu de décomposer l’espace en écran, on va diviser le temps T en N segments δt et on somme entre chaque segment sur l’ensemble des états accessibles (pour retrouver nos trous).

On va ainsi réécrire en notation de Dirac la superposition de tous les chemins possibles d’un instant δt à un autre (en découpant discrètement T dans un premier temps). On approxime à la Leibniz chacun de nos chemins en un ensemble de segments droits, puis on réduira la longueur des segments...

On obtient :

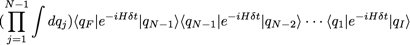
C’est bien égal à notre amplitude de départ puisqu’on reconnaît la relation de fermeture :

où le 1 désigne la matrice identité.

Remarque : la relation de fermeture assure que l’ensemble des états lq> est complet, ou dit autrement, que les états lq> pavent tout l’espace. Tout état Iq> se décompose donc sur l’ensemble des vecteurs de base de l’espace des q. Et comme Iq><qI est le projecteur sur Iq> qui opère cette décomposition, il est normal que notre Iq> décomposé soit égal à notre Iq> de départ (puisqu’on projette sur une base). La relation de fermeture donne donc bien l’identité.

En prenant l’Hamiltonien d’une particule libre :

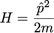
et en insérant :

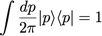
On obtient après intégration (en se rappelant que l’état position en représentation impulsion est une onde plane : < p I q > = e-ipq ) :

En rendant maintenant continue notre discrétisation du temps (δt→0) et en posant :

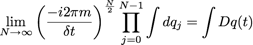
qui représente l’intégration sur l’ensemble des chemins Dq(t) joignant qI à qF.

On obtient :

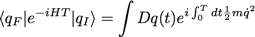
Et en partant de l’Hamiltonien général :

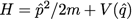
on a :

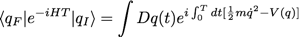
On reconnaît sous l’intégrale le Lagrangien qui émerge donc naturellement de l’Hamiltonien :

et on retrouve aussi l’action :

Conclusion : l’amplitude de probabilité qu’une particule se propage de qI à qF en un temps T est une somme le long de chaque chemin rejoignant qI à qF d’ondes planes dont la phase varie comme l’action entre 0 et T.

On préfère souvent, plutôt que les positions qI et qF, considérer de façon plus général un état initial I I > et final I F >. On cherche donc :

< F I e-iHT I I >. On retombe sur ce qu’on connaît en insérant à nouveau un jeu complet d’état :

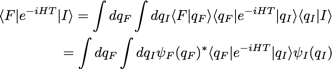
en mélangeant notation de Dirac et de Schrödinger.

C’est souvent intéressant de prendre pour état I et F, l’état fondamental I 0 >. On verra plus tard pour quelle raison (même si on peut déjà deviner qu’il va s’agir de normalisation).

Et on appelle Z l’amplitude < 0 I e-iHT I 0 >.

Il est aussi d’usage de remplacer t par -it («rotation de Wick»), pour d’obscurs (pour moi) raisons de rigueur mathématique visant à se débarrasser des complexes, ce qui donne :

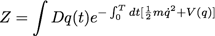
appelée intégrale de chemin euclidienne.

Voilà on en a fini !

Finalement :

pour obtenir l’amplitude de probabilité qu’une particule évolue d’un état à un autre en un temps T dans le formalisme des intégrales de chemin :

1. ➡on joint chaque couple de point de l’espace (qI et qF) par l’ensemble des chemins possibles entre eux.
   

2. ➡pour chaque chemin, on somme tout son long des termes oscillants (des ondes) dont la phase varie comme l’action de la particule sur la trajectoire suivie, puis on somme sur tous les chemins entre qI et qF :
   

3. ➡

   

   
   

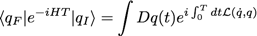
4. ➡on multiplie le résultat par le recouvrement entre état initial et état final aux coordonnées spatiales initiales et finales choisies pour le chemin :
   

5. ➡

   

   
   
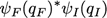
6. ➡on recommence pour un autre couple qI et qF et ainsi de suite jusqu’à avoir couvert tous l’espace pour chacun des états. Et on somme tous les résultats...
   

   

   
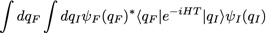
   On couvre ainsi l’ensemble du champ des possibilités pour qu’un état initial I aboutisse à un état final F.
   

7. ➡
   
   

Limite classique :

Un truc sympa avec le formalisme des intégrales de chemin est qu’on retrouve facilement la limite classique de la mécanique quantique.

On restaure d’abord la constante de Planck qu’on avait laissé tombée jusque là :

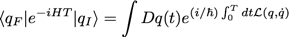
et on prend la limite :

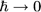
L’intégrale est totalement dominée par les valeurs stationnaires de la phase de l’exponentielle et on obtient :

où qc(t) est le chemin classique déterminé par la résolution de l’équation d’Euler-Lagrange (condition à la stationnarité de l’action) :

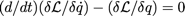
Tout chemin ne minimisant pas l’action voit sa phase varier très rapidement par rapport au chemin voisin. Et comme on superpose au final tous les différents chemins (= on somme les différentes phases) on se retrouve avec des amplitudes significatives sur la trajectoire classique seulement (là où des phases sensiblement égales, du fait de la stationnarité, s’accumulent). Partout ailleurs, les superpositions sont destructives...

On retrouve là bien sûr le principe de moindre action.

Création d’un champ

Tout ce qu’on a vu jusque là est valable pour une particule qui se ballade toute seule mais ce qu’on veut, nous, c’est des champs. D’ailleurs si le formalisme des intégrales de chemin semble avoir peu d’utilité pour une particule, on voit rapidement que pour un champ, l’histoire des intégrations sur l’ensemble de l’espace prend de l’intérêt puisque le champ lui-même, occupe tout l’espace. Dans un autre formalisme, on serait amenés à devoir tout sommer, autant que le «formalisme» s’en occupe directement.

Il faut d’abord qu’on crée un champ, c’est-à-dire un matelas de masselottes et ressorts comme dans le préambule. Finalement, ce n’est qu’une collection de particules qa liées entre elles (l’indice a servant à garder mentalement trace de la position de chacune).

Imaginons donc un réseau de particules distantes de l et liées les unes aux autres (c’est notre matelas).

Z reste le même :

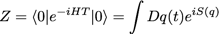
C’est l’action qui change. Il nous reste à trouver le nouvel Hamiltonien.

En imaginant qu’il y a N particules, il devient :

Et on va prendre le même potentiel que décrit plus haut :

Gommons maintenant notre discrétisation de l’espace (l →0). On remplace l’indice a par un vecteur position à 2 dimension :

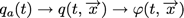
(traditionnellement, on utilise des lettres grecques plutôt que latines pour désigner des champs).

La fonction φ(t,x) est notre champ !

Rq : x est un paramètre en théorie des champ, il ne fait qu’indexer les masselottes, et pour ne pas le confondre avec une variable dynamique comme q ou φ, on a choisi q plutôt que x pour désigner la variable dynamique position.

Continuons à prendre la limite continue :

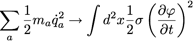
où σ est la masse surfacique.

Il nous reste à arranger le potentiel. C’est le qaqb qui nous gène mais comme :

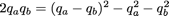
Et en supposant que kab ne connecte que les voisins les plus proches :

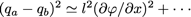
(la dérivée spatiale est prise dans la direction joignant a et b)

En arrangeant encore un tantinet les choses (petit changement de variables pour faire apparaître la célérité c), on obtient :

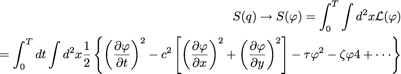
Et l’invariance de Lorentz émerge naturellement ! On utilisera d’ailleurs maintenant la notation d’Einstein :

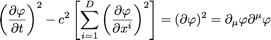
On prendra toujours T→∞ = intégration sur tout l’espace-temps :

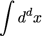
(où d=D+1 pour généraliser notre D=2 du départ)

Finalement, pour avoir l’amplitude de probabilité de transition entre deux états quantiques avec les intégrales de chemin, la recette est :

1. ➡imposer une symétrie suivant la physique qu’on veut faire.
   Ici, invariance de Lorentz pour faire de la physique des particules.
   

2. ➡choisir le champ suivant la façon dont on veut qu’il se transformation sous les symétries.
   Ici, on a choisi un champ scalaire φ.
   

3. ➡puis écrire l’action qui en découle en jetant toute puissance supérieure à deux dans les dérivées (car on ne sait pas les gérer, c’est-à-dire quantifier).
   

4. Ici, ça nous donne :
   

5. ➡

   

   
   

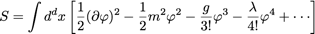
6. où les facteurs numériques sont choisis pour leur utilité.
   

7. ➡on voit là la force des symétries. Imposer l’invariance de Lorentz et des puissances inférieures ou égales à deux dans les dérivées astreint le Lagrangien à avoir la forme précise :
   

8. ➡

   

   
   

9. où V est un polynôme en φ. Et si par exemple, on ajoute que la physique est symétrique pour φ→-φ, alors on n’a plus que des puissances paires dans V...
   

10. ➡Enfin : l’intégrale de chemin d’une théorie des champs scalaires en dimension d d’espace-temps s’écrit :
    

11. ➡

    

    
    

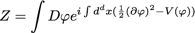
12. on notera que la théorie quantique des champs à (0+1) dimension n’est que la mécanique quantique.
    

Finalement, on a eu besoin de l’objet champ pour maintenir la symétrie de l’espace-temps. La particule ↔ perturbation du champ n’est ainsi plus un danger pour les symétries, le problème d’une théorie Lorentz-invariante est réglé en amont.

Limite classique :

Une nouvelle fois, on l’obtient facilement en rétablissant la constante de Planck et en la faisant tendre vers zéro :

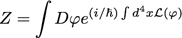
et à nouveau, on évalue Z par la méthode de la phase stationnaire où on cherche les extrema de l’action, ce qui donne les équations d’Euler-Lagrange :

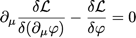
et on retrouve bien sûr les équations de champ classique, ce qui donne dans notre théorie scalaire :

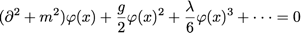
Perturbation du vide :

L’intégrale de chemin obtenue correspond à un champ dans son état fondamental (entre deux états I 0 >), qui même s’il est bourré de fluctuations quantiques, n’est pas très intéressant. En effet, en théorie quantique des champ, on va mesurer les énergies à partir de cet état zéro(quitte à retrancher une quantité infinie dans le Lagrangien).

Ce qu’on veut, c’est donc pouvoir perturber notre champ pour y voir naître et mourir des particules (il nous faut des sources et des puits).

Revenons à notre matelas fait de masselottes. Le perturber revient à secouer une ou plusieurs masselottes et cela correspond à ajouter dans le potentiel des termes de la forme Ja(t)qa qui deviennent J(x)φ(x) en théorie des champs.

J(t,x) est la fonction source, elle décrit comment le matelas est perturbé. Et en rebondissant sur le matelas, on peut obtenir des paquets d’onde allant d’un endroit à l’autre. Cela correspond bien à notre idée de sources et puits de particules.

On ne sait calculer cette intégrale fonctionnelle que dans le cas où :

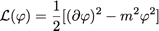
On parle alors de théorie de champ libre.

L’équation du mouvement qui en sort est :

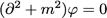
équation de Klein-Gordon. Etant linéaire, elle se résout facilement et donne :

avec :

On est en unité naturelle où ħ=1 et donc où fréquence se confond avec énergie et vecteur d’onde avec impulsion. Ayant ça en tête, on reconnaît la relation énergie-impulsion pour une particule de masse m (version sophistiquée du célèbre E=mc2). On comprend pourquoi on a appelé m le coefficient devant le φ2. Et on s’attend donc à ce que cette théorie de champ décrive une particule relativiste de masse m. Chouette !

Ajoutons maintenant notre terme de source et tentons de résoudre :

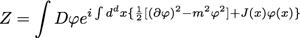
En se démenant un peu dans les calculs (une technique consiste, après une intégration par partie, à faire des aller-retour mentaux entre un réseau discret et la version continue afin de jouer avec des matrices plutôt qu’avec des opérateurs), on trouve :

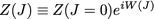
avec

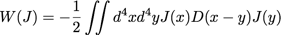
Où D(x) est appelé propagateur et joue un rôle essentiel en TQC. C’est l’inverse d’un opérateur différentiel (mathématiquement, c’est une fonction de Green) et on l’obtient en résolvant :

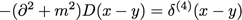
D est forcément une fonction de x-y et non de x et y séparément puisqu’aucun point de l’espace n’est spécial (homogénéité).

On peut calculer D en passant dans l’espace des impulsions et en utilisant le théorème des résidus pour intégrer sur un contour dans le plan complexe.

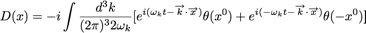
avec :

Physiquement, D(x) décrit l’amplitude de probabilité pour qu’une perturbation du champ se propage de l’origine à x.

Finalement, ce vide perturbé est une modulation du vide sans perturbation  :

On obtient bien le produit entre le vide non perturbé ( Z(J=0) ) et une oscillation dont la phase est fonction de la perturbation. Cette phase W(J) est l’action du champ avec Lagrangien perturbé sur la trajectoire φ(x) solution des équations d’Euler-Lagrange.

Rq : La dernière affirmation se démontre, mais restons-en là, ça semble somme toute plutôt logique. En effet, Z est une l’amplitude de transition et on a vu qu’on l’obtenait en sommant sur toutes les trajectoires d’espace-temps possibles des termes oscillants ayant l’action sur la trajectoire comme phase. Si un terme l’emporte, c’est celui correspondant à la trajectoire extrémisant l’action, comme plus haut quand on a regardé la frontière entre quantique et classique... De toute façon, le terme eiW(J) s’éclairera d’avantage un peu plus loin.

Revenons à D(x). Comme on s’est placé dans le cadre de la relativité restreinte, on espère un comportement drastiquement différent si x est à l’intérieur ou à l’extérieur du cône de lumière.

Prenons d’abord un point dans le cône (t,x=0), avec t>0, on a alors :

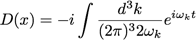
On obtient donc un comportement oscillatoire = on est content.

Pour un point à l’extérieur du cône, disons ( t = 0 , x ), on obtient (en posant θ(0)=1/2) :

La racine carrée est coupée pour une impulsion égale à ± im et l’intégration donnera donc une exponentielle décroissante en ∼ e-mIxI (intégration dans le plan complexe). On a bien changement de comportement et on découvre une chose étonnante :

si classiquement, une particule ne peut sortir du cône de lumière, un champ quantique peut s’écouler à l’extérieur sur une distance de l’ordre de m-1, c’est à dire de l’ordre de la longueur de Compton associé à la masse m (h/mc en rétablissant les constantes). 

Rq : W(J) n’est que quadratique en J alors que Z(J) comprends des puissances arbitrairement grandes. Cela aura son importance quand on parlera de diagrammes de Feynman.