Première chose qui m’a bêtement longuement perturbé :

Pourquoi, pour une température donnée, le maximum de la distribution de densité d’énergie par m (en longueur d’onde) émise par un corps noir ne correspond pas au maximum de la distribution par Hz (en fréquence).

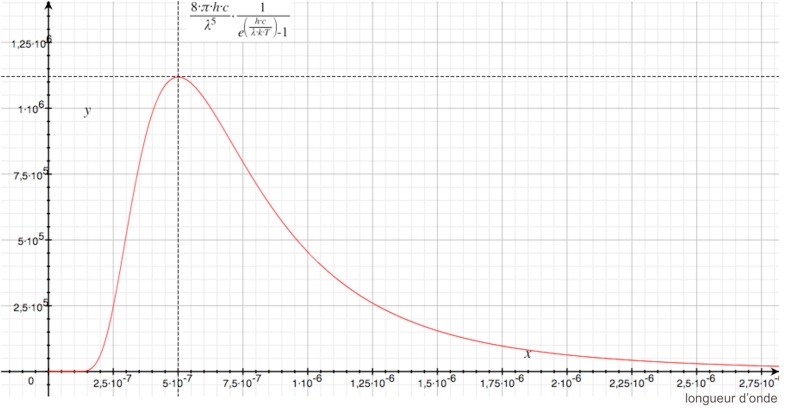
Mon erreur était d’oublier ce que représentait réellement la courbe et je tenais ce raisonnement simpliste : un maximum est un maximum et donc le maximum en fréquence devrait correspondre au maximum en longueur d’onde via la conversion λ=c/ν.

Mais voilà, les deux courbes sont bien différentes. Regardons la densité d’énergie en longueur d’onde : c’est la quantité d’énergie émise entre des longueurs d’onde régulièrement espacées (axe des abscisses). On disperse le spectre à l’aide d’un réseau et on enregistre le rayonnement reçu en fonction de la longueurs d’onde. Or la longueur d’onde est inversement proportionnelle à la fréquence. En avançant régulièrement sur l’axe des longueurs d’onde, les fréquences correspondantes diminuent et surtout se resserrent de plus en plus ! Conséquence, comme la descente après le maximum de la distribution d’énergie est relativement douce alors que les fréquences correspondantes se rapprochent, on conçoit facilement que la concentration en fréquence pourra se trouver maximisée un peu plus loin (en longueur d’onde équivalente) que le max de la distribution en longueur d’onde.

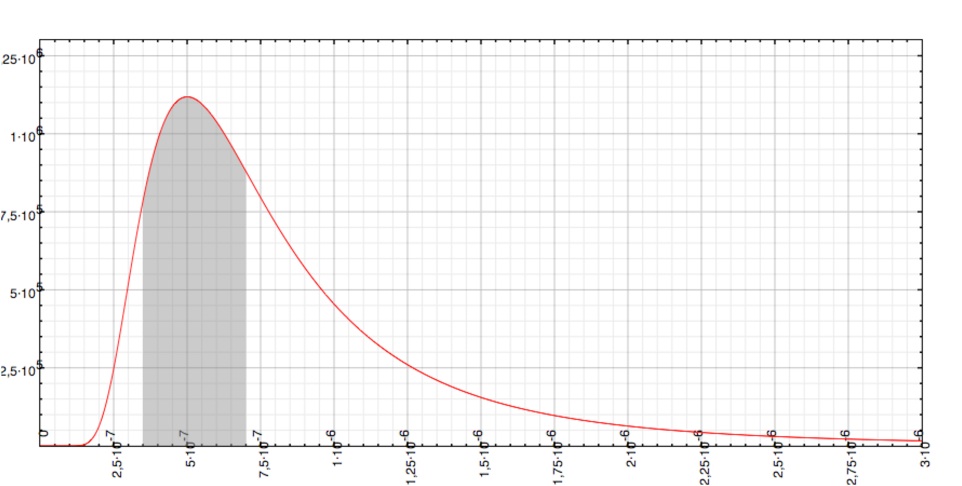
Le maximum en fréquence va donc bien être déplacé par rapport au maximum en longueur d’onde.

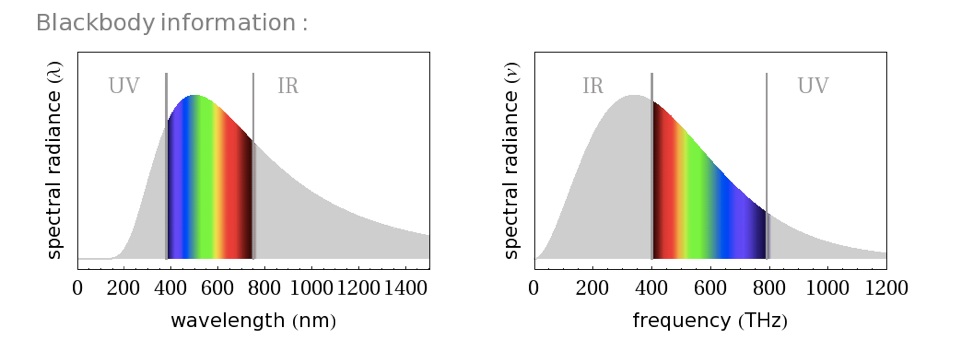
Et voilà ci-dessus la répartition du spectre visible sur les deux distributions avec le soleil comme corps noir (T≈6000 K). La densité en longueur d’onde est centrée sur le visible alors que la densité en fréquence est centrée sur les infra-rouges proches. Un détecteur fonctionnant sur une certaine fenêtre de longueur d’onde (à dλ près) se centrerait donc plutôt sur le visible pour recueillir le maximum d’énergie alors qu’un détecteur utilisant des transitions énergétiques (qui se font, du moins c’est ce que j’ai d’abord supposé, à dE ou, de manière équivalente, à dν près) se décalerait, lui, sur l’infrarouge proche. Cela semble devoir impliquer que des cellules photovoltaïques aient une meilleure sensibilité avec un gap dans l’infrarouge. Or, ce n’est pas le cas, le mauvais rendement du Si est d’ailleurs imputé à son maximum de sensibilité dans l’infrarouge proche et non dans le visible (voir, par exemple, cette conférence). Ces détecteurs ne travaillent-ils donc pas à dν près, c’est-à-dire linéairement en fréquence ? On dirait que non...

Indice de cette non linéarité : le resserrement des niveaux au fur et à mesure de l’augmentation de l’énergie.

Un semiconducteur de meilleur rendement que le Si s’obtiendrait en translatant le gap vers le visible seulement si sa largeur est fixée en longueur d’onde. Cette fenêtre va par contre s’élargir en énergie (cf. l’exemple ci-dessous).

Considérer les bandes d’absorption comme des cavités résonnantes spatiales semblent aller dans le sens d’une linéarité en longueur d’onde plutôt qu’en fréquence. On cale une longueur d’onde entre chaque niveau d’énergie n. L’énergie de chaque niveau augmente donc en 1/n !

Illustrons l’amélioration possible du rendement d’un semiconducteur après décalage vers le visible d’une fenêtre d’absorption de largeur constante en longueur d’onde, d’abord centré sur 0,9 μm :

Le corps noir est pris à 6000 K et on compare l’énergie émise entre 0,7 et 1,1 μm (centrée sur le pic en fréquence), à celle émise entre 0,3 et 0,7 μm, centrée sur le pic en longueur d’onde :

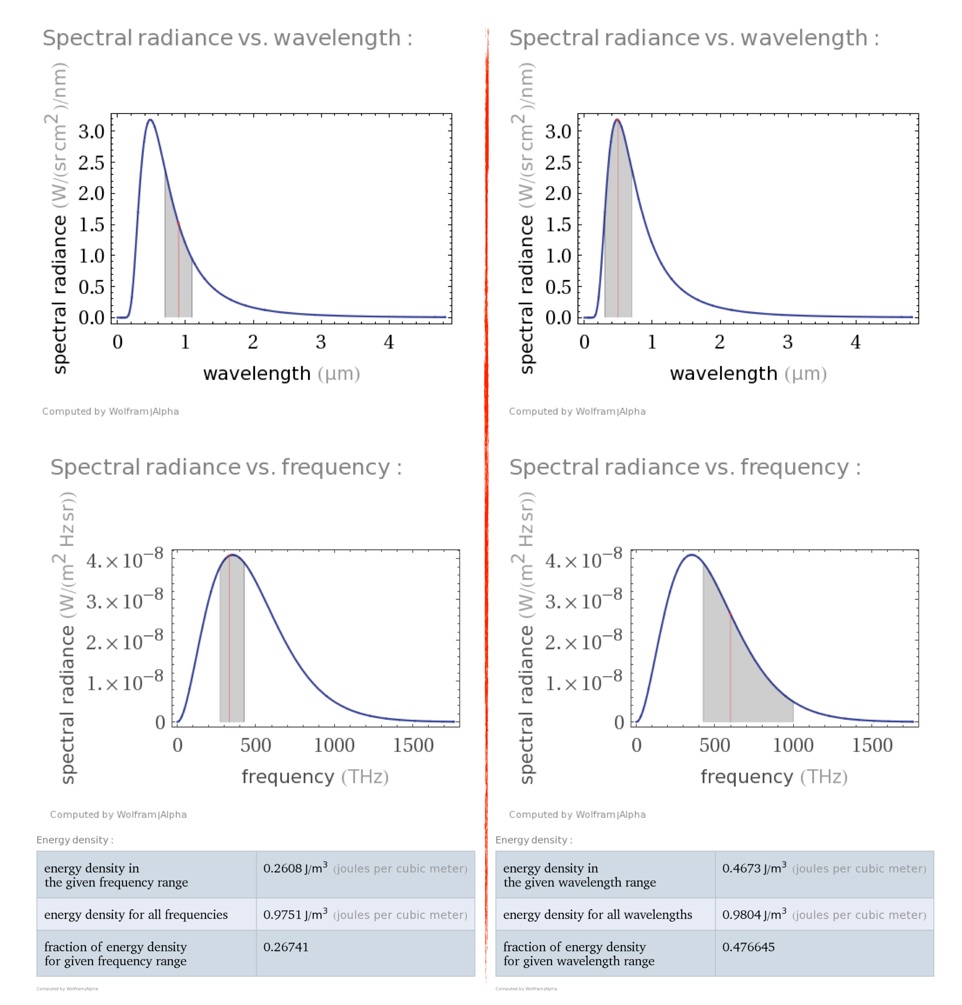
Regardons maintenant la sensibilité spectrale de nos yeux :

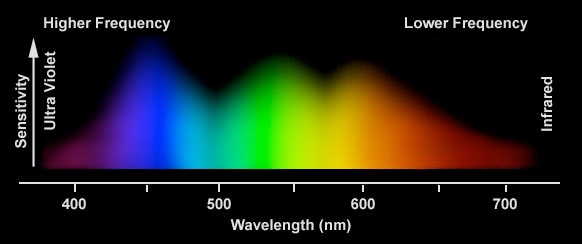
La plage spectrale de sensibilité de nos yeux (= la lumière visible) est centrée sur le maximum de la distribution en longueur d’onde du soleil. Quel est l’intérêt évolutif ?

Question similaire (mais préalable) : pourquoi la photosynthèse se fait-elle sur le spectre visible ? Optimisation de l’énergie ?

➥Réponse probable : il semblerait que l’appareil de mesure biologique photosensible (pigments organiques pour la photosynthèse ou nos yeux) se moque de la densité en énergie par longueurs d’onde. Cela ne serait qu’une coïncidence (l’ennemi du mauvais scientifique) ! la sensibilité recouvre le max en longueur d’onde de la distribution spectrale du soleil, soit, mais la réelle contrainte environnementale ayant sélectionné cette fine plage de longueurs d’onde serait sans doute la courbe d’absorption de l’eau. En effet, ces pigments se sont constitués quand toute vie se trouvait encore dans les océans. Et cela peut expliquer pourquoi cette plage de sensibilité de nos yeux (que se partagent à peu près toutes les bestioles) est si étroite ; la voie induite au départ nous a coupé les passages vers d’autres plages de longueurs d’onde.

Article entrant dans les détails : Some paradoxes, errors, and resolutions concerning the spectral ...

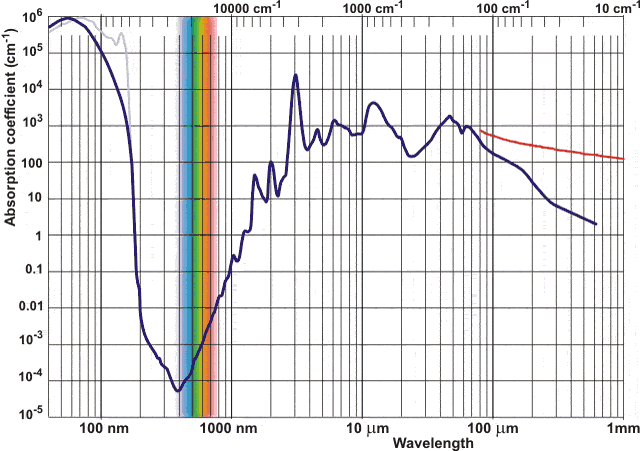
source de la courbe : http://www.lsbu.ac.uk/water/vibrat.html#d