Ondes gravitationnelles

La courbure de l’espace-temps modifie la propagation d’une onde mais elle peut elle-même en générer !

La relativité générale tient évidemment compte du déplacement à vitesse limitée de toute perturbation. Cette nécessité de causalité associée à la continuité de l’espace-temps l’élève au rang de champ élastique. Ainsi, une modification de l’espace-temps à un instant et en un lieu donné doit pouvoir se propager de proche en proche d’où la prédiction d’ Einstein de l’existence d’ondes gravitationnelles parcourant l’univers. Mais l’immense rigidité de «l’élastique» rend leur observation très difficile.

Une analogie entre ondes gravitationnelles et ondes électromagnétiques permet de cerner points communs et différences.

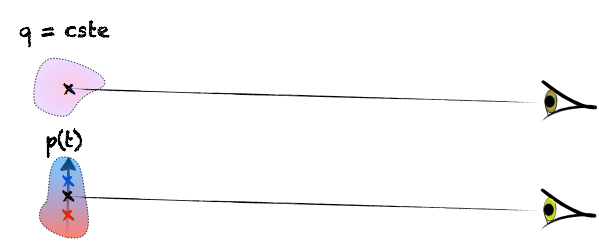
Pour simplifier les choses, on va se placer loin des sources de ces ondes. On a donc une distribution (de charges pour l’électro-magnétisme, d’énergie pour la gravitation) éloignée de l’observateur. Et on veut que cette distribution varie.

➡ monopôles

Dans les deux cas, pas moyen de faire disparaître et réapparaître tout ou partie de la distribution. En effet, charge ou énergie se conservent.

Traduction :
pas de monopôle électrique ni gravitationnel.
Conséquence :
pas d’onde scalaire (spin 0).

➡ dipôles

Dans le cas gravitationnel, on ne peut pas non plus bouger le centre de masse ni faire tourner la distribution par conservation du moment cinétique et angulaire.
Traduction : pas de dipôle gravitationnel.
Conséquence : pas d’ondes gravitationnelles vectorielles.

Dans le cas électromagnétique, il en va autrement...
Bien qu’on ne puisse toujours pas bouger le barycentre des charges, l’existence de charges négatives permet de splitter la distribution. En effet, une charge négative se déplaçant vers le haut devant être compensée par une charge positive se déplaçant vers le bas, on peut très bien séparer la distribution de charges en deux pôles.

Traduction :
les dipôles électromagnétiques peuvent générer des ondes.
Conséquence :
les ondes électromagnétique sont vectorielles (spin 1).

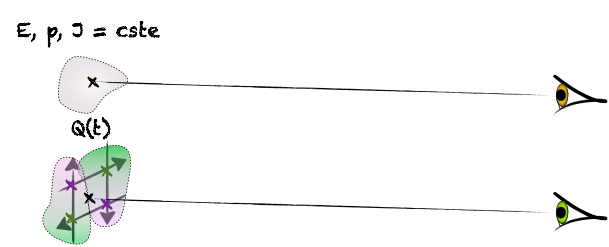
➡ quadrupôles

On est toujours à la recherche de quelque chose qui pourrait varier dans la distribution de charges vue par l’observateur. On est maintenant amené à décomposer le mouvement dans deux directions et voir si ce mouvement permet de conserver tout ce qui doit l’être :

•rien ne doit apparaître ou disparaître (conservation scalaire)
•le centre de masse ne doit pas bouger (conservation vectorielle).

Pas de problème si les deux mouvements s’annulent deux à deux.

Traduction :
les quadrupôles de la distribution de masse peuvent générer des ondes gravitationnelles.
Conséquence :
les ondes gravitationnelles sont tensorielles de rang 2 (spin 2).

Regardons maintenant ce que cela implique sur l’onde produite. Et montrons d’abord que l’existence d’ondes gravitationnelles est implicite dans les équations d’Einstein.

Si on perturbe un peu un espace-temps plat, on a pour métrique (appelée métrique de champ faible) :
gμν = ημν + hμν
avec | hμν |≪1

hμν doit être symétrique. Ça nous laisse tout de même 10 éléments indéterminés...

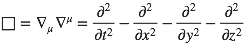
On a dans ces cas là besoin d’une jauge pour les fixer (on veut restreindre l’espace des coordonnées à l’aide d’une symétrie intéressante). Et ici, on aimerait que notre perturbation aboutisse à un d’Alembertien

un truc se propageant quoi...

Il suffit d’aller butiner là par exemple pour voir qu’une telle jauge existe, c’est la jauge de Lorenz (et 36 autres noms) :

En remplaçant g par notre métrique presque plate, on obtient :

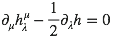
où h est la trace hνν
Le passage à la forme «trace reverse» (transformation du tenseur permettant d’automatiquement respecter l’équation de continuité) permet de simplifier l’écriture :

La jauge de Lorenz s’écrit maintenant :

L’équation d’Einstein devient, en champ faiblement perturbé et dans le vide (on injecte la métrique de champ faible dans Gμν , on applique la jauge et on prend
Tμν = 0) :

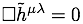
Conclusion : une faible perturbation du champ gravitationnel se propage comme une onde !

Remarque :

•On parle aussi de forme linéarisée des équations d’Einstein
•on obtient la forme «plate» du d’Alembertien car notre espace de base est plat.

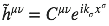
Dans tel cas, on est amené à chercher des solutions sous forme de complexes oscillants (on prend la partie réelle à la fin) :

où kσ est le vecteur d’onde.

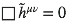
devient alors :
kαkα = 0

Donc pour être solution de l’équation d’Einstein linéarisée, le vecteur de l’onde plane doit être de type lumière. Cela revient à peu près à dire que les ondes gravitationnelles se propagent à la vitesse de la lumière.

D’autre part, la jauge de Lorenz permet d’écrire que :
kμCμν = 0
Donc l’onde gravitationnelle est transverse.

Cela donne 4 nouvelles contraintes sur nos coefficients. Il en reste 6 indéterminés... Mais plus pour longtemps. Choisissons une direction pour la propagation, disons les z, et hop, déjà 4 autres de parties.

Et enfin, en imposant une trace nulle, nous voilà bien ! Et pourquoi une trace nulle ? Lors de l’établissement des équations d’Einstein, on a vu qu’un espace vide d’énergie (Tμν = 0) entraînait la nullité de la courbure scalaire et du tenseur de Ricci. Heureusement pour ce qui nous intéresse ici, ça ne veut pas dire que l’espace est sans courbure mais que celle-ci se cache à coup sûr en dehors de la diagonale.
Si on veut que notre perturbation se propage dans le vide, c’est donc naturel de la supposer sans trace.

Remarque :

Il en est de même pour la source de ces ondes ; ce sont les termes non diagonaux du tenseur énergie-impulsion qui peuvent les créer. Les radiations gravitationnelles sont donc des ondes de cisaillement. Les termes de pression, s’ils ne s’annulent pas, doivent être asymétriques puisque ça revient à avoir des termes de cisaillement non nuls. En effet, écraser dans une direction et étirer dans la direction perpendiculaire est équivalent à un cisaillement à 45° de ces 2 directions.

Autre remarque :

Au final, on a affiné notre jauge avec la condition de non-trace ; on est maintenant dans la jauge TT (transverse traceless gauge), sous-jauge de la jauge harmonique.

À quoi ressemble finalement notre onde maintenant qu’on a circonscrit sa forme ?

Le tenseur Cμν a cette tête :

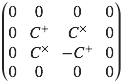
On retrouve bien une symétrie quadrupolaire et les deux coefficients C+ et C× correspondent aux deux polarisations + et × que peuvent prendre ces ondes comme on va le voir.

Considérons dans un plan transverse à la direction de propagation de l’onde (z = cte) deux particules séparées sur l’axe des x d’une distance dx. La distance les séparant va évoluer lors du passage de l’onde comme :

soit

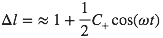
Et de même, pour deux particules séparées de dy, on obtient :

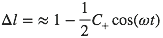
puisque Cyy = -C+

Donc pendant que les x sont étirés, les y sont contractés et puis ça s’inverse... On peut représenter ainsi l’effet de l’onde sur un ensemble de masses test disposées en cercle sur un plan transverse.

On comprend mieux le nom de polarisation +. Et on constate que l’effet de l’onde est celui d’une force de marée. C’est naturel puisque l’onde gravitationnelle n’est qu’un gradient gravitationnel variant dans le temps, et une force de marée n’est elle-même rien d’autre qu’un gradient gravitationnel.

Ça c’était pour les C+... Et les C× alors ? Facile, c’est la même chose mais tourné à 45°.

Ce sont les deux modes indépendants de polarisation linéaire des ondes gravitationnelles.

On peut aussi transformer nos deux modes perpendiculaires + et × en des polarisations circulaires vers la droite ou vers la gauche en les combinant :

Remarquons que les particules ne voyagent pas sur l’anneau mais ne font que dessiner des petits cercles.

Dans chaque cas que le mode est invariant par rotation de 180°, ce qui va avec la nature quadripolaire et le spin 2 de ces ondes.

Ce qui marche avec des petites masses flottant dans l’espace marche en réalité avec n’importe quel corps solide ou liquide car comparée à la rigidité de l’espace, celle de la matière est plutôt ridicule.
Cela a amené des projets de détection reposant d’abord sur les résonances que les ondes gravitationnelles pourraient faire naître dans des barres métalliques, jusqu’ici sans succès, puis à d’immense dispositifs interférentiels en croix tentant d’atteindre une précision suffisante pour la détection d’effets spectaculairement infimes comme on va le voir.

Première chose, reconnectons les ondes à leur source, l’énergie :

Équation analogue à celle de l’électrodynamique relativiste où

joue donc le rôle de A :

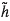
Et comme pour l’électrodynamique, la solution prend la forme d’un potentiel retardé (on utilise les fonctions de Green pour y arriver) :

où

Avec :

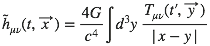
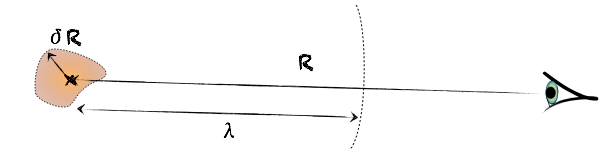
•x ≡ R ≫ δR, où δR détermine l’étendue de la source (intervalle de variation de y) = on se place loin par rapport à l’étendue de la source.
Cela permet d’écrire : 1/|x-y|≈1/R
•λ ≫ δR, c’est l’hypothèse de mouvement lent, c’est-à-dire que les vitesses internes dans la distribution de masse sont petites devant c. Pour un mouvement oscillant, ça correspond bien à v ≈ δRω ≪ c, donc λ ≫ δR.
Cela permet d’écrire : t-y/c = t-R/c

On obtient :

S’ensuivent deux, trois tours de passe-passe avant que n’apparaisse glorieusement :

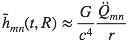
où les points sur la tête désignent les dérivées temporelles et où Qμν est le moment quadrupolaire de la distribution de masse :

On a donc retrouvé notre prévision de départ, ouf... L’amplitude de l’onde dépend bien de l’accélération (oscillation) du moment quadrupolaire de la distribution de charge et on a même précisé les choses.

Les tours de passe-passe :

déjà, on n’a besoin que de la partie spatiale. En effet, la jauge de Lorenz nous permet d’écrire :

, et donc

ce qui donne, en passant dans l’espace de Fourier (rappelons que h oscille) :

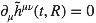
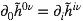
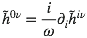
Donc pas de problème pour retrouver la partie temporelle une fois qu’on a la spatiale.

Rq : on peut passer impunément d’indices bas à des indices haut sur

, un des bienfait de la jauge TT.

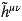
on va donc commencer par :

on intègre par partie

Le premier terme est nul puisque la source est circonscrite et

par conservation de Tμν.

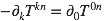
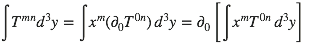
et retour pour un tour :

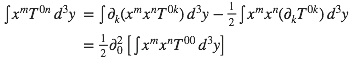
Et T00 vaut en première approximation ρ (là, on passe sous silence «l’auto-induction» de l’onde sur la source qui modifie sa densité d’énergie).

G/c4, c’est riquiqui ! D’où la galère pour détecter des ondes gravitationnelles ; il nous faut des sources bien lourdes et qui gigotent vite. Les systèmes binaires d’étoiles à neutron ou de trous noirs sont bien des candidats sympathiques... mais si éloignés qu’on se retrouve avec une amplitude h de l’ordre de 10-20, et avec de la chance encore. Comme h est le morceau de métrique qui fait la variation par rapport à un espace plat, ça donne au niveau du détecteur :

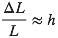
où ΔL est l’allongement ou le raccourcissement dû au passage de l’onde.
Et on se retrouve à devoir mesurer des variations relatives de longueur de l’ordre de 10-20... Et encore s’agit-il de sources très puissantes et rares.

Petit calcul d’ordre de grandeur pour le système Terre-Lune :
Q ∼ mR2, m est la masse réduite, soit quasiment la masse lunaire dans ce cas, et R vaut à peu près la distance Terre-Lune.
∼ ω2mR2 et par la 3ème loi de Newton Mω2R=GM2/(2R2) où M, somme des 2 masses vaut quasiment la masse terrestre. On trouve donc :
h ∼ MT ML G2/d RT-L c4
Si on regarde depuis Mars à seulement 100 million de km, on sera amené à détecter des amplitudes d’environ 10-26 ! Bon courage.

La première idée pour obtenir une telle précision fut d’utiliser la résonance d’une barre métallique ; il suffit d’attendre qu’une onde de la bonne fréquence daigne venir résonner. Bien sûr, on isole la barre des vibrations terrestre, on la met dans un frigo, on la couple avec un système amplificateur, etc. Il y a de ces barres un peu partout et on a rendu hommage à leur papa en les nommant barre de Weber.
Jusque là, elles sont restées silencieuses... mais aux aguets (dès qu’une étoile assez proche explose, c’est pour elle).

Autre idée : utiliser des interféromètres lasers (Michelson) avec des très grands bras. Un grand L permet de rendre ΔL plus accessible. Les deux principaux sont l’américain LIGO (bras de 4 km) et l’européen Virgo (3 km). Il ne leur reste plus qu’à détecter une variation d’environ 10-17 m...
Pour faciliter les choses, des projets d’interféromètres spatiaux comme LISA attendent leur financement.

Ces détecteurs doivent permettre une observation directe des ondes gravitationnelles, mais font jusqu’à maintenant chou blanc.
On pourrait même finir par douter de leur existence par une nuit sans lune mais non, rassurez-vous, il y a bien eu détection, mais indirecte pour le coup. Bien qu’indirecte, sa précision en fait l’un des tests les plus fort de la relativité générale et a apporté un prix Nobel à ceux qui l’ont permis : Russell Alan Hulse et Joseph Hooton Taylor. Raison officielle : «la découverte d'un nouveau type de pulsar, une découverte qui a ouvert de nouvelles possibilités pour l'étude de la gravitation» (prix Nobel 1993).
Mais avant d’évoquer ce triomphe, il faut parler de l’énergie rayonnée.

Evidemment que les ondes gravitationnelles transportent de l’énergie puisqu’elles courbent l’espace ! Et donc fatalement, la distribution de masse perd de l’énergie par émission radiative.
Par analogie avec l’électrodynamique, la puissance rayonnée doit dépendre du carré de la dérivée temporelle de l’amplitude du champ, en valeur moyenne.

Remarque :

C’est un résultat tout à fait général. C’est le cas, entre autres, du vecteur de Poynting électromagnétique (en fonction du potentiel vecteur A).
Plus généralement, si Tμν est l’énergie du champ, alors l’énergie totale sur une surface Σ de temps constant (= boule 3D) s’écrit :

Et pour le flux d’énergie rayonné, on intègre du T0m.
Or, le Tμν d’un champ est toujours quadratique en dérivés première de l’amplitude du champ. Remarquons que c’est effectivement ce qu’on a trouvé pour l’énergie d’un champ scalaire !
Grossièrement, un champ lie une contrainte à une déformation. La contrainte correspond à une gradient de la déformation et l’énergie est classiquement vu comme le scalaire formé par le produit du taux de déformation (vitesse) par la contrainte (force). Finalement, on a bien une forme quadratique entre deux dérivées premières (une spatiale et une temporelle). Ajoutons à cela que pour des oscillations harmoniques, dérivées spatiales et temporelles sont proportionnelles. Rien de choquant alors à avoir une puissance rayonnée qui va dépendre du carré de la dérivée temporelle de l’amplitude du champ.

On a donc

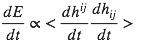
L’énergie perdue par l’émission d’ondes gravitationnelles vaut alors :

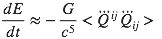
C’est la formule du rayonnement dipolaire d’Einstein dévoilée en 1918.

Jouons un peu avec les unités pour obtenir un ordre de grandeur. On peut déjà renverser le ridicule G/c5 en injectant le rayon de Schwarzschild RS = 2GM/c2, rayon minimal pour une boule de masse M donnée (c’est le rayon d’un trou noir).
Comme ∼ ω3mR2 ,

∼ -G/c5×ω6m2R4 = c5/G×(RS/R)2×(v/c)2
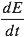
où v ∼ ωR est la vitesse caractéristique de la distribution de masse.

c5/G est maintenant un monstre d’environ 1052 Watts. Sans surprise, pour s’en rapprocher, il faut des sources le plus dense possible (R→RS) et des vitesses internes énormes (v→c).

Avec le système Terre-Lune, si loin de ces canons, un petit microwatt seulement est dissipé... Vraiment peanuts, surtout quand on sait que les marées dissipent à elles seules environ 3 terawatts ! Avec le système Terre-Soleil, on monte à une centaine de watts emportée par les ondes gravitationnelles, toujours pas terrible. Mais passons aux choses sérieuses avec un système binaire d’étoiles à neutrons, chacune d’environ une masse solaire, séparées par 10 secondes lumière : on arrive alors à 1032 W, beaucoup plus que le rayonnement électromagnétique du soleil (1026 W) !

Ce n’est pas anodin de dissiper autant d’énergie, ça freine. Et que se passe-t-il si on freine quelque chose en orbite (exercice classique de taupin) ? Il se rapproche et accélère (il tombe quoi). Les deux astres vont alors spiraler l’un vers l’autre de plus en plus vite et l’énergie rayonnée n’en devient que plus phénoménale. La phase finale de coalescence de tels systèmes représente d’ailleurs un des grands espoirs de source d’ondes gravitationnelles détectable.

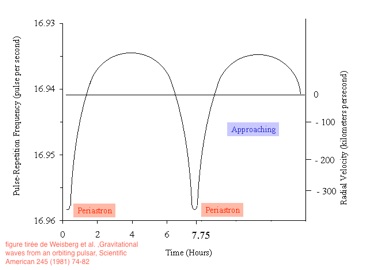
C’est là qu’on en revient à Hulse et Taylor. Ils ont découvert le premier système binaire d’étoiles à neutron, baptisé d’un joli PSR B1913+16, dont l’une des deux est aussi un pulsar. Or le pulsar, véritable phare sidéral, est un astre très précieux pour le physicien puisqu’il envoie avec une régularité extrême une salve d’ondes radio à chaque rotation (qu’il a rapide : pour le notre 59 ms). Et ce signal permet de tout savoir : période, vitesse radiale par rapport à nous, taille de l’orbite et son excentricité, donc les masses.

Comment un signal rythmique donne-t-il accès à tout ça ?

•l’effet Doppler va altérer le rythme de réception au cours de la révolution suivant que le pulsar se rapproche ou s’éloigne → on a la période ;

•toujours grâce à l’effet Doppler, on obtient la vitesse radiale du pulsar (par rapport à la terre), comme le ferait un radar sur la route ;
•la différence entre quantité de signaux décalés vers le bleu et quantité décalés vers le rouge nous donne l'excentricité ;
•les temps d’arrivée des signaux vont varier périodiquement suivant que l’émetteur est plus proche ou éloigné de la terre → on a l’orbite.

On peut donc faire le calcul de l’énergie emportée par les ondes gravitationnelles et en conclure théoriquement le taux de diminution de la période de révolution, chose aisément mesurable.
La figure suivante montre les données compilées en 2004 par Taylor et Weisberg (Relativistic Binary Pulsar B1913+16: Thirty Years of Observations and Analysis) et qui s’étendent sur presque 3 décennies. La période diminue donc bien mais ce qui frappe le plus est l’accord entre les données et la théorie 0,2% ! Et encore, cette incertitude est dominée par l’imprécision sur la vitesse du centre de la galaxie...

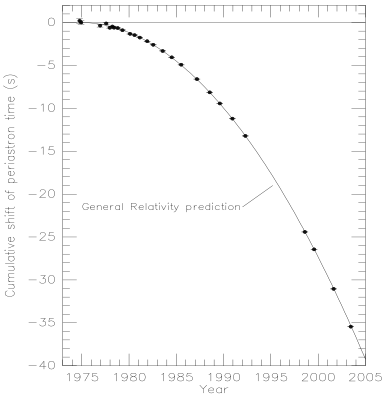
C’est quoi cette histoire de «shift of periastron» ?

Le décalage de la période due à la radiation d’ondes gravitationnelles est minuscule, 76 millionième de seconde par an ! Cela reste mesurable mais l’astuce du périastre rend les choses bien plus spectaculaire, et améliore donc l’incertitude.

En effet, le périastre est le point de l’orbite du pulsar le plus proche de l’étoile à neutron et quand la période est modifiée et que les étoiles se rapprochent, l’orbite est reconfigurée et le périastre évolue non linéairement avec le temps.

Au premier ordre en t, la phase de l’orbite varie comme :
où f0 correspond à f(t=0), fréquence mesurée au début des mesures.
Comme est très faible, le développement est très bon !
Or le pulsar atteint le périastre au temps tp tel que :

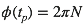
Par conséquent, l’instant tp du périastre se décale en :

Et cette augmentation en carré du temps permet d’arriver à des décalages conséquents.
Comme

et en prenant

= 76.10-6 s et T0 = 7,75 h
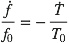
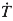
On obtient bien, au bout de 30 ans, un décalage négatif (une avance) d’environ 40 s !

On pourrait aussi se demander si, cerise sur le gâteau, le système binaire ne pourrait pas s’approcher bientôt de la phase de spiralage finale pour devenir détectable. Mais là, va falloir être patient... À raison de 3,5 m par an, il va falloir attendre 300 millions d’années.

Et dernière question, pas mal hors sujet : comment se fait-il que la lune s’éloigne, elle ?
Certes le système Terre-Lune dissipe pas mal d’énergie (surtout la Terre dans ses océans) mais une petite partie de cette énergie des marées n’est pas perdue mais transférée de la rotation propre de la Terre (qui ralentit) à la révolution de la Lune (qui s’écarte). Les forces de marée agissent comme une force de rappel qui synchronise les rotations des astres.